沖縄 職業訓練 平成26年度 試験問題と解答 問題【５】

平成26年度に沖縄県で行われた職業訓練の選考試験で出題された試験問題と、その解答と解説です。 本ページでは数学問題の設問【５】のみ記載しています。数学問題の設問【１】～【４】に関しては、次のページを参照してください。

沖縄 職業訓練 平成26年度 試験問題と解答 問題【１】
沖縄 職業訓練 平成26年度 試験問題と解答 問題【２】
沖縄 職業訓練 平成26年度 試験問題と解答 問題【３】
沖縄 職業訓練 平成26年度 試験問題と解答 問題【４】

具志川職業能力開発校、浦添職業能力開発校 共通

【５】図のように放物線①：Ｙ＝ａＸ² と直線②：Ｙ＝Ｘ＋２が、Ｘ座標の小さい方から順に２点Ａ、Ｂで交わっている。点ＡのＸ座標が－１であるとき、次の問に答えなさい。

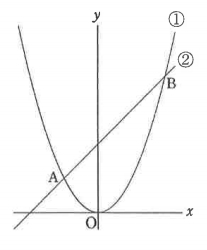
[問題1]ａの値を求めなさい。

[問題2]直線②とＹ軸との交点をＣとするとき、△ＯＢＣの面積を求めなさい。

解答と解説

試験問題１の解答：ａ＝１
まずは、点Ａの座標を求めます。点ＡのＸ座標は問題より－１と分かっているので残るＹ座標を求めます。点Ａは直線②上の点なので、Ｘ＝－１を直線②の式に代入するとＹ座標がもとまります。

　直線②：
　Ｙ＝Ｘ＋２
　Ｙ＝－１＋２＝１

よって、点Ａの座標は、(－１, １) と分かりました。また、点Ａは放物線①上の点でもあるので点Ａ(－１, １)を通ります。よって、この座標を放物線①の式に代入すると求めたいａの値が出てきます。

　放物線①：
　Ｙ＝ａＸ²
　１＝ａ(－１)²
　１＝ａ

よって、ａ＝１
放物線の式は、Ｙ＝Ｘ²

試験問題２の解答：２

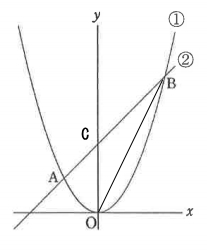
△ＯＢＣの面積を求めるには、点ＢとＣの座標を求める必要があります。

点Ｂの座標
点Ｂの座標は、点Ａと同じく直線②と放物線①の交点です。よって、直線の式を放物線の式に代入することで座標を求めることができます。

　放物線①：Ｙ＝Ｘ²
　直線②：Ｙ＝Ｘ＋２

直線②の式を放物線①に代入します。

　Ｘ＋２＝Ｘ²
　Ｘ²－Ｘ－２＝０

これを因数分解すると

　Ｘ²－Ｘ－２＝０
　(Ｘ－２)(Ｘ＋１)＝－　
　Ｘ＝２、－１

Ｘの値は２と－１と分かりました。－１は、点Ａですね。よって、点ＢのＸ座標は２だと分かります。これを放物線①もしくは、直線②の式に代入すると点ＢのＹ座標も出てきます。

　放物線①：
　Ｙ＝Ｘ²
　Ｙ＝２²＝４

よって、点Ｂの座標は(２, ４)

点Ｃの座標
点Ｃの座標は、直線②とＹ軸との交点なので、Ｘ＝０はすぐに分かります。これを直線②の式に代入するとＹ軸の値もわかります。

　直線②：
　Ｙ＝Ｘ＋２
　Ｙ＝０＋２＝２

よって、点Ｃの座標は(０, ２)

補足：
Ｙ＝Ｘ＋ａという直線の式がある場合、Ｙ軸と交わる点(切片)は、ａとなるということを知っていれば上のようなＣ点を求める計算は不要。

三角形ＯＢＣの面積
三角形ＯＢＣの面積は、下図のように辺ＯＣを底辺、点ＢからＹ軸までの距離を高さとして計算することができます。

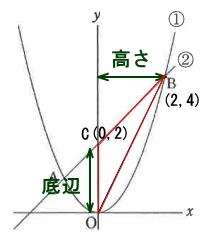
底辺の長さは、点ＣのＹ座標になるので２、高さは点ＢとＹ軸の距離なので点ＢのＸ座標になります。よって、その長さは２となります。このことより、三角形ＯＢＣは

底辺の長さ２、高さ２の三角形なのでその面積は、

　三角形ＯＢＣの面積＝２×２÷２＝２

※解説の内容が不明、不十分というのがあればコメントをください。