大阪 職業訓練 試験問題 数学-問4(平成27年5月21日実施) 普通課程

平成27年5月21日に大阪で実施された職業訓練の選考試験問題 問4の解説です。大阪で行われる職業訓練の試験問題は、筆記試験ではなく毎回、選択方式ですが試験時間が短いためこれらの過去問を繰り返し実施し、短時間かつ正確に解けるようにしておきましょう。

問1～3に関しては以下のページに解説をまとめているので参考にして下さい。

大阪 職業訓練 試験問題 数学-問1
大阪 職業訓練 試験問題 数学-問2
大阪 職業訓練 試験問題 数学-問3

図で、1辺4cmの立方体ABCD-EFGHの辺CDとBCとBFの中点をそれぞれ点P、点Q、点Rとして、この立方体を3点P, Q, R を通る平面で切り、2つの立体に分けることを考える。このとき、次の各問の答えとして正しいものをア～オの中から1つ選び、記号で答えなさい。

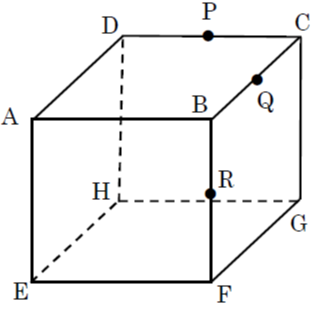
[問題1]　切断面の形を求めよ。

[問題2]　切断面の面積を求めなさい。

[問題3]　切り分けられた2つの立体のうち、点C を含む立体の体積を求めよ。

解答と解説

試験問題１の解答：オ
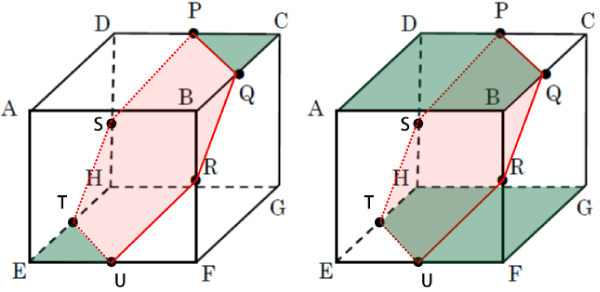
この問題で間違いやすいのが、単純に点PQRをそれぞれ結んで切り口は二等辺三角形と答えてしまいやすい点です。まず、点PQを通る線分PQからナイフを入れ、点Rを通るように切り込んでいくとナイフが点Rに達したとき、下図のようにナイフは点D、点Hの中点Sも通ります。

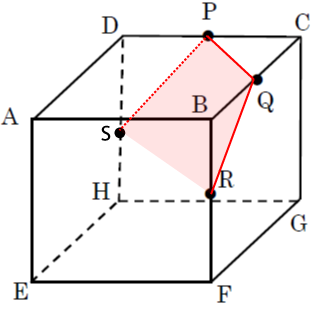
更に切り込んでいくとナイフは、点E、点Hの中点T、および点E、点Fの中点Uを通って立方体を2つに分断します。

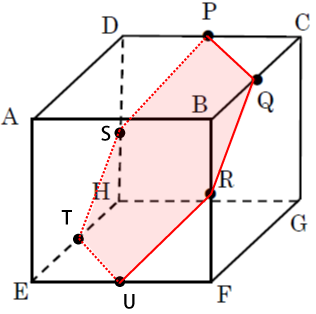
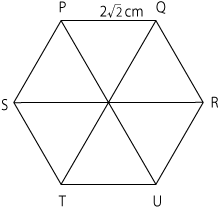
よって、その時の切り口は点PQRUTSの6カ所を通ります。各中点間の距離は等しいので切り口は正六角形だと分かります。

解答：オ

試験問題２の解答：ア
この問題を特にあたり知っておかなければならないのが「三平方の定理」です。三平方の定理は、図形が直角三角形の場合、以下の式が成り立つというもの。

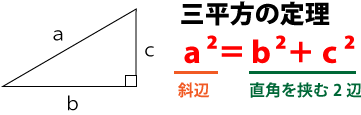
まずは、切り口の正六角形の一辺PQの長さを求めます。辺PQ以外でも構いません。立方体の一辺の長さは問題文より4㎝と分かっているので、三角形CQPは線分CP、線分CQが2㎝の直角二等辺三角形だとわかります。ここで三平方の定理を使います。

ａ²＝ｂ²＋ｃ²
PQ²＝2²＋2²
PQ²＝8
PQ＝√8
PQ＝2√2

よって、線分PQの長さは2√2

■正六角形の面積を求める
正六角形の中には、一辺の長さが2√2の正三角形が6つあります。よって、正三角形の面積の求め方を知っていればこの問題は簡単に解くことができます。

[公式を使った解き方]
正三角形の面積を求める公式は次の通り。

面積＝(√3/4)xａ²

よって、正三角形の面積は次の通りになります。

面積＝(√3/4)x(2√2)²
　　＝(√3/4)x8
　　＝2√3

正六角形の中には、この正三角形が6つあるので、正六角形の面積は次の通りになります。

面積＝2√3 x 6
　　＝12√3 cm²

[公式を使わない解き方]
三平方の定理(ａ²＝ｂ²＋ｃ²)のみを使って解きます。

正六角形の中には一辺が2√2の正三角形が6つ入ります。その正三角形を更に半分にすると直角三角形ができます。

この直角三角形の底辺の長さは√2。高さが不明なのでこれを三平方の定理で求めます。

ａ²＝ｂ²＋ｃ²
(2√2)²＝(√2)²＋Ｃ
Ｃ²＝(2√2)²－(√2)²
Ｃ²＝8－2
Ｃ²＝6
Ｃ＝√6

よって、直角三角形1個の面積は次の通り。

面積＝√2x√6÷2
　　＝√12/2
　　＝2√3/2
　　＝√3

この直角三角形が全部で12個あるので求めたい正六角形の面積は次の通り。

正六角形の面積＝√3x12
　　　　　　　＝12√3 cm²

試験問題３の解答：ウ
切り取ってできた2つの立体の上面と下面について見てみます。

点Cを含む立体の上面の三角形CPQと、もう一方の立体の下面の三角形ETUは等しい三角形です。更に点Cを含む立体の下面の五角形GHTUFと、もう一方の立体の上面の五角形ABQPDは等しい五角形です。更にその他の各辺の長さも等しいので、この二つの立体は合同だと言えます。

よって、元々の立方体の体積を1/2したものが切り取り後の立体の体積になります。

元々の立方体の体積
4x4x4＝64㎝³

切り取り後の立体の体積
64÷2＝32㎝³

※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容も不明であれば遠慮なくコメントください。