問1~3に関しては以下のページに解説をまとめているので参考にして下さい。
図は、三角柱ABC-DEFであり、BC=BE=2cm、 AB=4cm、∠ABC=90°である。このとき、以下の問い にア~オから選んで答えなさい。
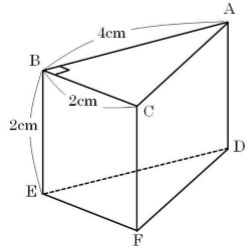
[問題1] 辺ACの長さを求めなさい。
[解答群]
ア 3cm イ 4cm ウ 2√3cm エ 2√2cm オ 2√5cm
[問題2] 3点 B、D、Fを頂点とする△BDFの面積を求めなさい。
[解答群]
ア √10cm² イ 6cm² ウ 2√10cm² エ 4cm² オ 9cm²
[問題3] 3 点 B、D、Fを含む平面と点Eとの距離を求めなさい。
[解答群]
ア √2cm イ 2√2cm ウ √3cm エ 4/3cm オ 5/2cm
解答と解説
試験問題1の解答:オ
三角形ABCは直角三角形なので、三平方の定理が使用できます。
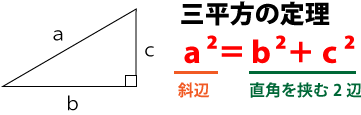
a²=b²+c²
AC²=AB²+BC²
AC²=4²+2²
AC²=20
AC=√20
AC=2√5 ㎝
試験問題2の解答:イ
辺BDの長さを求める
辺BDの長さを三平方の定理を使用して求めます。ED=4㎝なので、辺BDの長さは次の通り。
a²=b²+c²
BD²=BE²+ED²
BD²=2²+4²
BD²=20
BD=√20
BD=2√5 ㎝
辺BFの長さを求める
辺BFの長さを三平方の定理を使用して求めます。BE=EF=2㎝なので、辺BFの長さは次の通り。
a²=b²+c²
BF²=BE²+EF²
BF²=2²+2²
BF²=8
BF=√8
BF=2√2 ㎝
辺DF=辺ACなので、辺DFは問題1より2√5㎝だと分かります。更に辺DFと辺BDが2√5で等しいので、三角形BDFは二等辺三角形だと分かります。点Dから辺BFへ垂線を下した点を点Qとします。DQは、三角形BDFの高さとなるのでこれが求まれば三角形BDFの面積が出てきます。
BQはBFの半分の長さなので、√2㎝となります。三平方の定理を使ってDQの長さを求めます。
三平方の定理
a²=b²+c²
BD²=BQ²+DQ²
(2√5)²=(√2)²+DQ²
DQ²=20-2
DQ=√18
DQ=3√2
よって、三角形BDFの面積は次の通り。
△BDFの面積=2√2x3√2÷2
△BDFの面積=6 ㎝²
試験問題3の解答:エ
問題文は少し不親切ですが、平面BDFと点Eとの距離とは、点Eから平面BDFに垂線を下した最短距離のこと。言い換えると、三角形BDFを底面、点Eを頂点とした三角錐の高さにあたります。三角形BDFを底面、点Eを頂点とした三角錐は、三角形DEFを底面、点Bを頂点とした三角錐でもあります。文章だけでは分かり難いので必ず、図形を書くようにしましょう。
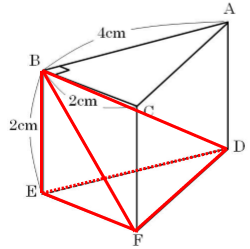
よって、まずは三角形DEFを底面、点Bを頂点とした三角錐の体積を求めます。
△DEFの面積=EFxDE÷2
=2×4÷2
=4㎝²
三角錐の体積=底面積x高さ÷3
=4×2÷3
=8/3 ㎝³ ・・・(1)
よって、三角形DEFを底面、点Bを頂点とした三角錐の体積は8/3 ㎝³
求めたいのは三角形BDFを底面、点Eを頂点とした三角錐の高さ。体積は、三角形DEFを底面、点Bを頂点とした三角錐の体積と同じなので8/3 ㎝³。三角形BDFの底面積は問題3より、6㎝²だと分かっています。よって、以下の式が成り立ちます。
三角錐の体積=底面積x高さ÷3
8/3=6x高さ÷3
高さ=8/6
=4/3 ㎝
※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容も不明であれば遠慮なくコメントください。

