この問題は平成30年4月入校(試験実施日:平成30年2月16日)の大阪職業訓練普通過程(高校卒業程度)の選考試験問題問3の解説です。
中学卒業レベルの短期課程の問題とは異なり、普通課程は高校卒業レベルになるため問題レベルが一気に高くなります。そのため、事前に予習して行く人として行かない人とでは大きな差が出るため、当サイトで解説している過去問を繰り返し実施し、しっかりと解けるようにしておきましょう。
実際の試験の問題用紙は以下のページで確認することができます。
⇒大阪府職業訓練校試験問題(平成30年度2月16日実施 普通課程)
問1、問2、問4に関しては以下のページに解説をまとめているので参考にして下さい。
問3 試験問題
下図のように半径 3cm の円 O が 2 直線と A、B で接している。 AP=BP=10cm のとき、以下の問いに答えなさい。
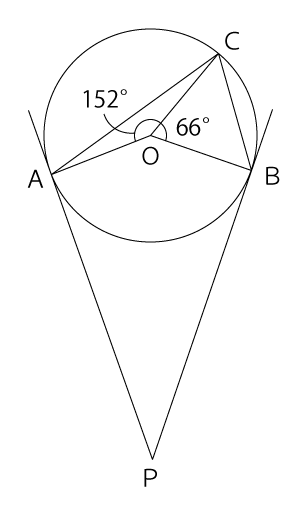
[問題1] ∠OCB の大きさを求めなさい。
[解答群]
- 44°
- 53°
- 57°
- 60°
- 66°
[問題2] ∠APB の大きさを求めなさい。
[解答群]
- 29°
- 30°
- 33°
- 35°
- 38°
[問題3] 四角形 AOBP の面積を求めなさい。
[解答群]
- 15 cm²
- 18 cm²
- 25 cm²
- 30 cm²
- 33 cm²
解答と解説
解答と解説を記載していきます。
解き方が分からないという人を少しでも減らすためにできる限り分かり易く必要以上に細かく順を追って解説している部分がありますが、実際の試験時は丁寧に計算し過ぎると時間のロスに繋がるため、自分の分かるところは効率よく解答していくようにしてください。
問題1の解答と解説
試験問題1の解答:ウ
OCとOBは円の半径なので、△OBCは2等辺三角形になります。よって、∠OCBは次の通り。
∠OCB=(180-66)÷2
=114÷2
=57°
問題2の解答と解説
試験問題2の解答:オ
問題1と同様の方法で∠ACOを求めます。
∠ACO=(180-152)÷2
=28÷2
=14°
よって、∠ACBは次の通りになります。
∠ACB=57+14
=71°
∠ACBは中心角である∠AOBの円周角なので円周角の定理より以下の式が成り立ちます。
∠AOB=∠ACB×2
よって、∠AOBは次の通り。
∠AOB=∠ACB×2
=71×2
=142°
OAと円の接線APは必ず直角で交わるので∠OAP、∠OBPは90°だと分かります。よって、∠APBは次の通り。
∠APB=360-∠AOB-∠OAP-∠OBP
∠APB=360-142-90-90
=38°
問題3の解答と解説
試験問題2の解答:エ
下図のように線分OPを引くと、直角三角形OAPとOBPの2つの三角形ができます。
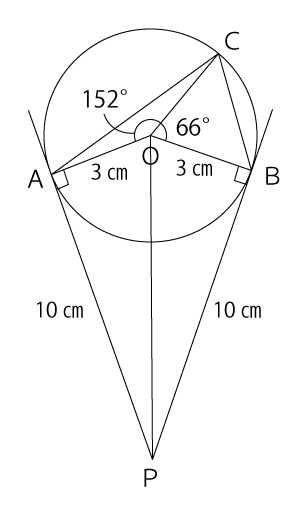
いずれの三角形も底辺が10cm、高さが3cmの直角三角形なので、面積は次のようになります。
△OAPの面積=△OBPの面積=10×3÷2
=15cm²
よって、四角形AOBPの面積は次の通り。
四角形AOBPの面積=△OAPの面積+△OBPの面積
=15+15
=30cm²
※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

