問1、問3~問4に関しては以下のページに解説をまとめているので参考にして下さい。
大阪 職業訓練 短期過程試験問題 数学-問1
大阪 職業訓練 短期過程試験問題 数学-問3
大阪 職業訓練 短期過程試験問題 数学-問4
次の文章題の答えとして正しいものをア~オの中から1つ選び、記号で答えなさい。
[問題1] 画用紙を何人かの生徒に配ったところ、1人に5枚ずつ配ると25枚余ったので、1人に6枚ずつ配ると12枚不足した。このときの生徒の人数を求めなさい。
[解答群]
ア 37人
イ 39人
ウ 41人
エ 43人
オ 45人
[問題2] 1から5までの数字を書いたカードが一枚ずつある。このカードを2枚選び、並べて2桁の整数をつくる。このとき2けたの整数が3の倍数になる確率はいくらになりますか。
[解答群]
ア 1/5 イ 1/4 ウ 3/10 エ 7/20 オ 2/5
[問題3] 2 次方程式X²+X-6=0の正の解が3X²+aX-6=0解でもあるとき、aの値を求めなさい。
[解答群]
ア a=-1 イ a=-2 ウ a=-3 エ a=1 オ a=2
[問題4] たかし君は家から5km離れたすすむ君の家に行くことになった。はじめ自転車に乗り時速16kmで15分進んだ。しかし自転車が故障したので、残りは歩くことにした。歩く速さを時速5kmとして歩いた時間を求めなさい。
[解答群]
ア 10分 イ 12分 ウ 14分 エ 16分 オ 18分
[問題5] 20から40までの整数のうち、素数であるものの平均を求めなさい。
[解答群]
ア 24 イ 26 ウ 28 エ 30 オ 32
解答と解説
試験問題1の解答:ア
求めたい生徒の人数をaとします。画用紙の枚数をbとします。
1人に5枚ずつ配ると25枚余ったということなので、生徒の人数aと画用紙の枚数bは次のように表すことができます。
b=ax5+25
b=5a+25 ・・・(1)
更に1人に6枚ずつ配ると12枚不足したということより、次の式が成り立ちます。
b=ax6-12
b=6a-12 ・・・(2)
(2)-(1)をすれば、生徒の人数aがでてきます。
b=6a-12
b=5a+25
————-
0=a-37
a=37
試験問題2の解答:オ
1枚目を10の位、2枚目を1の位のカードとします。逆でも構いません。10の位は5枚のカードから抜き出すので5通り。1の位は残り4枚から抜き出すので4通り。よって、組み合わせ総数は次の通り。
5×4=20
20通りの中から3の倍数となる数字は次の8通り
12、15、21、24、42、45、51、54
よって、確率は次の通り。
8÷20=8/20=2/5
試験問題3の解答:ウ
X²+X-6=0
(x+3)(x-2)=0
x=2、-3
正の解は2なので、3X²+aX-6=0 のXに2を代入します。
3X²+aX-6=0
3×4+2a-6=0
12+2a-6=0
2a=-6
a=-3
試験問題4の解答:イ
問題文を図に落とし込むと下図の様になります。
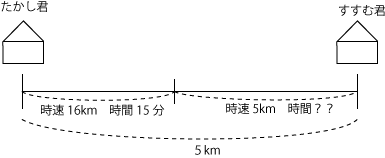
この問題を解くには時間、速度、距離の関係式を覚えておく必要があります。
速度=距離÷時間
また、単位に注意が必要。速度は”時速”で表されているのに対し、かかった時間は”分”で表されています。計算する場合は時間か分に統一して計算するようにすること。
自転車で進んだ距離は次の通り。
15分=1/4時間
速度=距離÷時間
16=距離÷(1/4)
16=距離x4
距離=4
よって、歩いた距離は1km(5km-4km)だとわかります。
歩いた時間は次の通り
速度=距離÷時間
5=1÷時間
時間=1/5
これを分に変換します。
60x(1/5)=12分
試験問題5の解答:エ
素数とは、1より大きい自然数で、約数が1と自分自身のみの数字のこと。
20から40までの整数のうち、素数であるものは次の4つ。
23、29、31、37
この4つの素数の平均は次の通り。
(23+29+31+37)/4=30
※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容も不明であれば遠慮なくコメントください。

