大阪 職業訓練 試験問題 数学-問4(平成28年8月26日実施) 短期課程

底面が1辺の長さ6の正方形ABCDで、側面が1辺の長さ6の正三角形4つでできている正四角すいO-ABCDがある。底面の対角線の交点をHとするとき、以下の問いにア～オから選んで答えなさい。

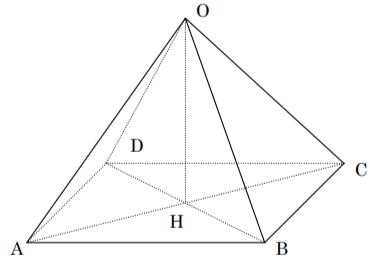
[問題1]　ABの中点をMとするときOMの長さを求めなさい。

[問題2]　三角すいO-ABCの体積を求めなさい。

[問題3]　△OAMのOMを回転の軸として回転させてできる立体の体積を求めなさい。

解答と解説

試験問題１の解答：エ
この問題を解くには、三平方の定理を利用します。

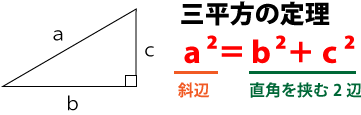
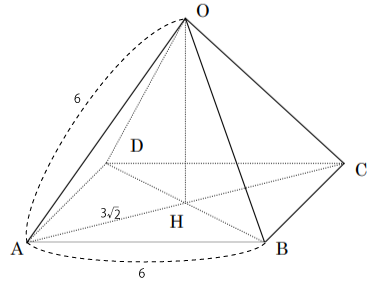
ABの中点をMとした場合、下図のようになります。

三平方の定理を利用すると、OMの長さが求まります。

OA²＝OM²+AM²
6²＝OM²+3²
36＝OM²+9
OM²＝27
OM＝√27
OM＝3√3

試験問題２の解答：ウ
∠AHB＝90°なので、三平方の定理を利用してAHの長さを求めます。直角二等辺三角形の比(1：1：√2)を用いるとより簡単。

AB²＝AH²+BH²

AH＝BHなので、上記式は次のようになります。

AB²＝AH²+AH²
6²＝2AH²
AH²＝18
AH＝√18
AH＝3√2

同様にOHの長さを求めます。

OA²＝OH²+AH²
6²＝OH²+(3√2)²
36＝OH²+18
OH²＝18
OH＝√18
OH＝3√2

三角錐の体積を求める
三角錐体積＝底面積ｘ高さ÷３

底面は△ABCなので底面積は次の通り。

底面積＝6ｘ6÷2
　　　＝18

三角錐体積＝底面積ｘ高さ÷３
　　　　　＝18ｘｘ3√2÷3
　　　　　＝18√2

試験問題３の解答：イ
△OAMのOMを回転の軸として回転させると下図のように円錐ができあがります。

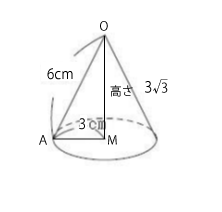
円錐の体積を求める公式は次の通り。

円錐体積＝底面積ｘ高さ÷３

底面は半径を3とした円なので体積は次の通りになります。

円錐体積＝底面積ｘ高さ÷３
　　　　＝(3ｘ3ｘπ)ｘ3√3÷3
　　　　＝9√3π

※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容も不明であれば遠慮なくコメントください。