大阪 職業訓練 試験問題 数学-問2(平成29年8月24日実施) 短期課程

問２ 試験問題

次の文章題の答えとして正しいものをア～オの中から1つ選び、記号で答えなさい。

[問題1]　300の約数の個数を求めなさい。

[問題2]　8％の食塩水と15％の食塩水と混ぜ合わせて、10％の食塩水を350g作りたい。8％の食塩水を何g混ぜればよいか求めなさい。

[問題3]　直線ｙ＝Ｘ/2-3 に平行で、点(-2,5)を通る直線の式を求めなさい。　

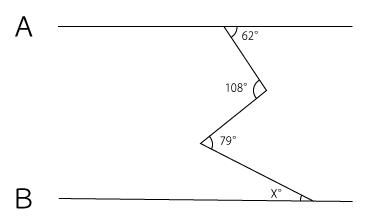
[問題4]　下の図でA//Bであるとき、∠Ｘの大きさ求めなさい。

[問題5]　AさんとBさんがじゃんけんを1回するとき、勝敗が決まる確率を求めなさい。

解答と解説

解答と解説を記載していきます。
解き方が分からないという人を少しでも減らすためにできる限り分かり易く必要以上に細かく順を追って解説している部分がありますが、実際の試験時は丁寧に計算し過ぎると時間のロスに繋がるため、自分の分かるところは効率よく解答していくようにしてください。

問題１の解答と解説

試験問題１の解答：エ
約数とは、300を割り切ることのできる整数のことで、この問題ではその個数を求める必要があります。

300程度の数であれば、力技で約数の個数を求めてもさほど時間はかかりませんが、大きい数値が出題された場合は素因数分解で導く方法を知っておく方が効率的なのでできる限り頭に入れておいてください。

まずは、300を素因数分解します。

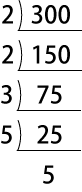
300＝2²×3¹×5²

約数の個数を求める場合、素因数分解した結果の指数部分を以下のように計算することで求めることができます。

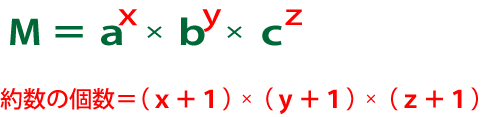
よって、求めたい約数の個数は次の通り。

300＝2²×3¹×5²
約数の個数＝(2+1)×(1+1)×(2+1)
　　　　　＝3×2×3
　　　　　＝18

実際の約数

300の実際の約数は以下の18こです。

300の約数＝｛1,2,3,4,5,6,10,12,25,15,20,30,50,60,75,100,150,300｝

問題２の解答と解説

試験問題２の解答：オ

食塩水の濃度を求める公式を知っていなくても、濃度と言えば普通に食塩水の中に何グラムの食塩が含まれているかと言うことくらいは直ぐに分かりますよね？

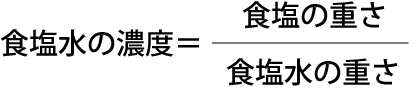
問題文から分かっている内容を図にまとめ、それぞれの容器をＡＢＣとする下図のようになります。

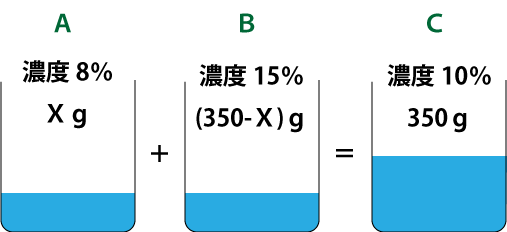
この問題で求めたいのは上図のＸです。
ここで、食塩の重さに着目して式を作ります。

Aの食塩の重さ＋Bの食塩の重さ＝Cの食塩の重さ

この式に実際に分かっている数値を当てはめると求めたいＸの値が出てきます。

(8/100×Ｘ)+{15/100×(350-Ｘ)}＝(10/100×350)
(2Ｘ/25)+{(1050-3Ｘ)/20}＝35
8Ｘ+5250-15Ｘ＝3500
7Ｘ＝1750
Ｘ＝250

問題３の解答と解説

試験問題３の解答：ア

直線の式『Ｙ＝ａＸ+ｂ』の『ａ』が直線の傾きだということを知っていれば、この問題は簡単に解くことができます。

求めたい直線は『Ｙ＝Ｘ/2-3』のグラフと並行ということなので求めたい直線の傾きは『Ｘ/2』だと分かります。よって、求めたい直線の式は次のようにあらわすことができます。

Ｙ＝Ｘ/2+ｂ

更にこの直線は点(-2,5)を通るということなのでＸ＝-2、Ｙ＝5を式に代入します。

Ｙ＝Ｘ/2+ｂ
5＝-2/2+ｂ
ｂ＝6

よって、求めたい直線の式は次の通り。

Ｙ＝Ｘ/2+6

問題４の解答と解説

試験問題４の解答：イ

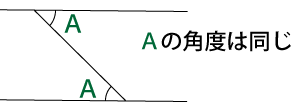
この問題を解くには以下のことを知っている必要があります。

下図のように線ＡＢと平行な線ＣＤを引き、上から順番に62°⇒46°⇒33°と求めていきます。

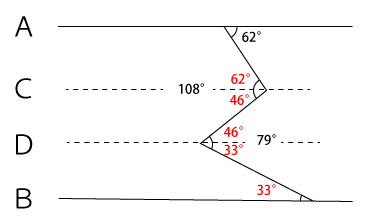
よって求める角度は、33°

問題５の解答と解説

試験問題５の解答：ウ

勝敗が決まる確率は、以下の式で求めることができます。

じゃんけんの総組み合わせ数＝3×3＝9通り

相子になる組み合わせは、『チョキとチョキ』、『パーとパー』、『グーとグー』の3通りのみ。よって、勝敗が決まる確率は次の通り。

勝敗が決まる確率＝(9-3)/9
　　　　　　　　＝6/9
　　　　　　　　＝2/3

じゃんけんの組み合わせ

じゃんけんの組み合わせを実際に書きだしてみます。

※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。