この問題は平成29年10月入校(試験実施日:平成29年8月24日)の大阪職業訓練短期過程の選考試験問題問4の解説です。
実際の試験の問題用紙は以下のページで確認することができます。
⇒平成29年10月入校 府立高等職業技術専門校 入校選考試験問題
問1~問3に関しては以下のページに解説をまとめているので参考にして下さい。
この問題を解くのに必要な知識
- 円の円周を求める公式【必須】
- 円の面積を求める公式【必須】
問4 試験問題
下の図のように、底面の中心をOとし、半径AO=6cmの円すいの頂点Bを固定して、平面上で転がすと、3回転して初めて点Aが元の位置に戻った。以下の問いにア~オから選んで答えなさい。ただし、円周率はπとする。
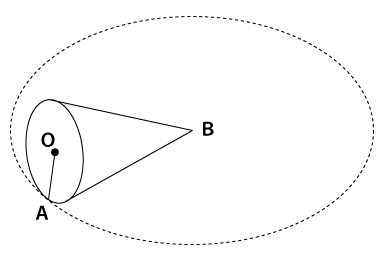
[問題1] 平面上で転がしたときにできる円の周の長さを求めなさい。
[解答群]
- 21π ㎝
- 36π ㎝
- 28π ㎝
- 32π ㎝
- 33π ㎝
[問題2] この円すいの側面積を求めなさい。
[解答群]
- 108π ㎝²
- 96π ㎝²
- 324π ㎝²
- 162π ㎝²
- 81π ㎝²
解答と解説
解答と解説を記載していきます。
解き方が分からないという人を少しでも減らすためにできる限り分かり易く必要以上に細かく順を追って解説している部分がありますが、実際の試験時は丁寧に計算し過ぎると時間のロスに繋がるため、自分の分かるところは効率よく解答していくようにしてください。
問題1の解答と解説
試験問題1の解答:イ
円すいの底面の円は半径6㎝。よって、この円の円周は次の通り。
円すいの底面の円の円周=(6+6)×π
=12π
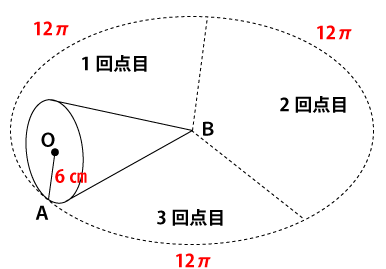
そして、この円すいが3回点して始めて元の位置に戻るということなので求める円の円周は次の通り。
求める円の円周=12π×3=36π
問題2の解答と解説
試験問題2の解答:ア
円すいの側面積は、円すいが1回点して動く部分の面積である下図の橙色に塗った部分に等しくなります。
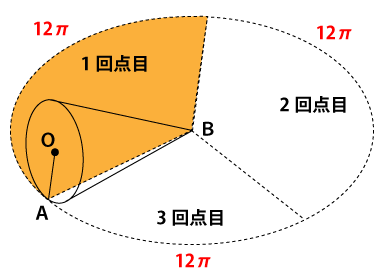
橙色の面積を求めるには、下図の円の面積を求めそれを1/3すればでてきます。問題1でこの円の円周が36πだとわかっているので、この円の半径は次のように求めることができます。
円の円周=円の直径×π
36π=円の直径×π
円の直径=36
よって、円の直径は36で、半径はその半分の18だと分かります。半径が分かればこの円の面積も求まりますよね。
円の面積=半壊×半径×π
=18×18×π
=324π
円すいの側面積である橙色の面積はこの円の面積の1/3なので次のようになります。
円すいの側面積=324π÷3=108π
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

