この問題は平成29年10月入校(試験実施日:平成29年8月24日)の大阪職業訓練短期過程の選考試験問題問3の解説です。
実際の試験の問題用紙は以下のページで確認することができます。
⇒平成29年10月入校 府立高等職業技術専門校 入校選考試験問題
問1~問2、問4に関しては以下のページに解説をまとめているので参考にして下さい。
この問題を解くのに必要な知識
- 三角形の相似条件
問3 試験問題
下の図のように、AB=9cm、AD=6cmである平行四辺形ABCDにおいて、∠DABの二等分線とBCを延長した直線との交点をGとする。また、AGと対角線BDの交点をE、AGとCDの交点をFとする。以下の問いにア~オから選んで答えなさい。
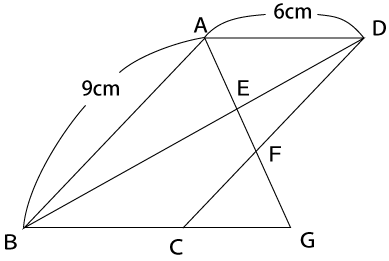
[問題1] △ABEと相似な三角形を答えなさい。
[解答群]
- △ADE
- △ABD
- △FDE
- △CDB
- △GBE
[問題2] CGの長さを求めなさい。
[解答群]
- 2㎝
- 3㎝
- 4㎝
- 5㎝
- 6㎝
[問題3] AFとFGの長さの比を求めなさい。
[解答群]
- 2:1
- 3:2
- 4:3
- 5:3
- 5:4
解答と解説
解答と解説を記載していきます。
解き方が分からないという人を少しでも減らすためにできる限り分かり易く必要以上に細かく順を追って解説している部分がありますが、実際の試験時は丁寧に計算し過ぎると時間のロスに繋がるため、自分の分かるところは効率よく解答していくようにしてください。
問題1の解答と解説
試験問題1の解答:ウ
この問題を解くには三角形の相似条件を知っておく必要があります。
三角形の相似条件
- 三角形の3組の辺の比がすべて等しい
- 三角形の2組の辺の比が等しく、その間の角が等しい
- 三角形の2組の角が等しい
向かい合う角(対頂角)は等しいので∠AEB=∠FEDだとわかります。また、辺ABと辺DCは平行なので平行線と角の関係から∠EAB=∠EFD、∠EBA=∠EDFだとわかります。
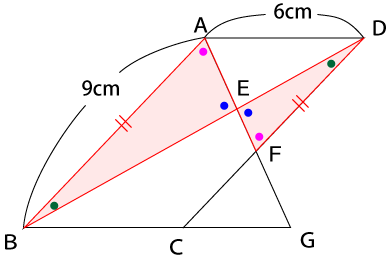
よって、三角形ABEと三角形FDEは3組の角が等しいことになるので三角形の相似条件『三角形の2組の角が等しい』を満たし、相似だとわかります。
問題2の解答と解説
試験問題2の解答:イ
問題文より線分AGは∠DABを二等分した線なので、∠DAE=∠ABAEだとわかります。また、線分ADと線分BGは平行なので、∠DAG=∠CGAになります。
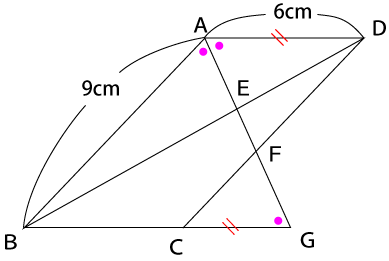
このことより、三角形ABGは二等辺三角形だとわかります。よって、線分BG=9㎝、さらに四角形ABCDは平行四辺形なのでAD=BC=6㎝です。
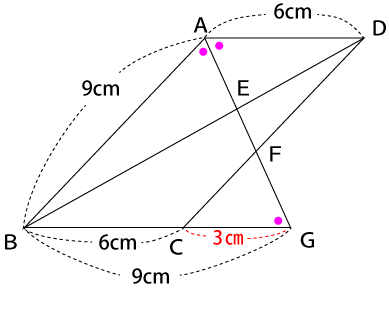
求めたい線分CGの長さは、9㎝-6㎝=3㎝となります。
問題3の解答と解説
試験問題3の解答:ア
三角形AFDと三角形GFCは3つの角が等しいため、相似三角形になります。
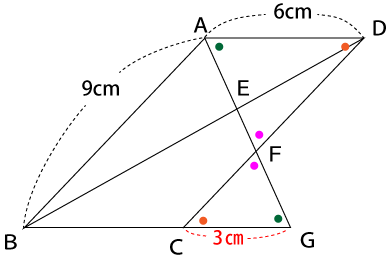
よって、各辺の比率はADとCGの長さから求めることができます。
AD:CG=6:3=2:1
よって、AFとFGの長さも2:1になります。
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

