この問題は平成29年10月入校(試験実施日:平成29年8月25日)の大阪職業訓練短期過程の選考試験問題問2の解説です。特に難しい問題はありませんが、間違いやすい問題もあるのでこれらの過去問を繰り返し実施し、短時間かつ正確に解けるようにしておきましょう。
実際の試験の問題用紙は以下のページで確認することができます。
⇒平成29年10月入校 府立高等職業技術専門校 入校選考試験問題
問1、問3~問4に関しては以下のページに解説をまとめているので参考にして下さい。
問2 試験問題
次の文章題の答えとして正しいものをア~オの中から1つ選び、記号で答えなさい。
[問題1] 195と585と1430の3つの数字の最大公約数を求めなさい。
[解答群]
- 60
- 65
- 70
- 75
- 80
[問題2] 下の図において、△ABEは正三角形であり、四角形BCDEは正方形である。∠xの大きさを求めなさい。
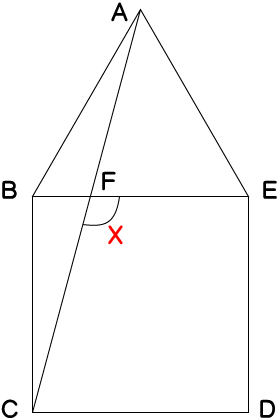
[解答群]
- 100°
- 105°
- 110°
- 115°
- 120°
[問題3] A,B,C,D,Eの現在の年齢はそれぞれ5歳、15歳、25歳、35歳、45歳である。A,B,Cの年齢の和の3倍が、D, Eの年齢の和の2倍に等しくなるのは、今から何年後か求めなさい。
[解答群]
- 5年後
- 10年後
- 15年後
- 20年後
- 25年後
[問題4] 原価1400円の品物に、30%の利益を見込んで定価をつけたが、売れないので定価の1割引きで売った。今の売価を求めなさい。
[解答群]
- 1368円
- 1680円
- 1764円
- 4200円
- 5040円
[問題5] ある船が、川を8㎞下ると1時間かかり、同じ距離上ると2時間かかった。この船の速さを求めなさい。
[解答群]
- 時速6㎞
- 時速6.5㎞
- 時速7㎞
- 時速7.5㎞
- 時速8㎞
解答と解説
解答と解説を記載していきます。
解き方が分からないという人を少しでも減らすためにできる限り分かり易く必要以上に細かく順を追って解説している部分がありますが、実際の試験時は丁寧に計算し過ぎると時間のロスに繋がるため、自分の分かるところは効率よく解答していくようにしてください。
問題1の解答と解説
試験問題1の解答:イ
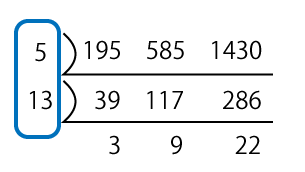
最大公約数=5×13=65
問題2の解答と解説
試験問題2の解答:イ
少し丁寧に解説しますが、実際は1~2分以内に解けるようにしておきたい問題です。
まずは、分かっている角度を図形に書き込んでいきましょう。
三角形ABEは正三角形と分かっています。三角形の1つの内角は60度ですよね。さらに四角形BCDEは正方形です。正方形の1つの内角は90度です。よって、これらの角度を図形に書き込むと下図のようになります。
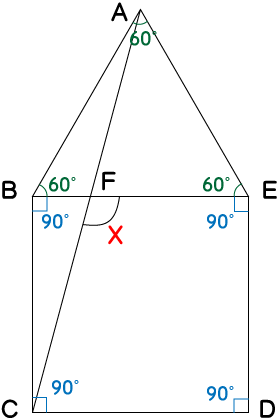
次に正三角形ABEと正四角形BCDEは、辺BEが共通なので各辺の長さ全てが共通の長さだと分かります。よって、辺ABと辺BCの長さも等しいことになるので三角形ABCは2等辺三角形ということになります。
三角形ABCの場合、∠BACと∠BCAは等しい角度だとわかります。
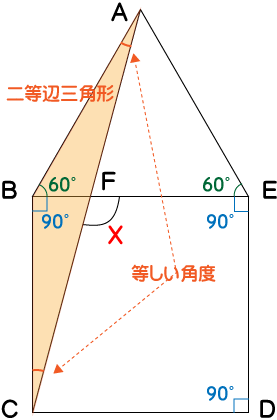
三角形の内角の和は180°、∠ABC=150°(60°+90°)と分かっているので∠BACと∠BCAは次のように求まります。
∠BAC+∠BCA+150°=180°
∠BAC+∠BCA=180°-150°
∠BAC+∠BCA=30°
∠BAC=∠BCAなので、∠BAC=∠BCA=15°だとわかります。これにより、∠BFCが求まります。
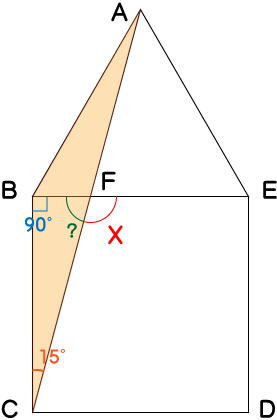
∠BFC=180°-∠FBC-∠BCF
=180°-90°-15°
=75°
よって、求めたい∠Xは次の通り。
∠X=180°-75°=105°
補足解答
少し丁寧に計算しましたが、∠Xは、∠FBCと∠BCFの和になります。これを『三角形の外角の定理』と言います。計算時間短縮に有効な法則なので頭にいれておきましょう。
∠X=∠FBC+∠BCF
=90°+15°=105°
問題3の解答と解説
試験問題3の解答:ア
求めたい答えをYと仮定します。
まずは、問題文から分かっていることを書きだします。
A=5歳
B=15歳
C=25歳
D=35歳
E=45歳
そして、Y年後のそれぞれの年齢は次の通りになります。
A=5+Y歳
B=15+Y歳
C=25+Y歳
D=35+Y歳
E=45+Y歳
また、問題文よりY年後は次の式が成り立つことが分かっています。
(A+B+C)×3=(D+E)×2
上の式にY年後の各自の年齢を代入すれば求めたいYの値が求まります。
(A+B+C)×3=(D+E)×2
{(5+Y)+(15+Y)+(25+Y)}×3={(35+Y)+(45+Y)}×2
{5+Y+15+Y+25+Y}×3={35+Y+45+Y}×2
{45+3Y}×3={80+2Y}×2
135+9Y=160+4Y
9Y-4Y=160-135
5Y=25
Y=5
よって、求めたい答えは5年後
問題4の解答と解説
試験問題4の解答:ア
若干の引っ掛け問題です。
問題文の『30%の利益を見込んで…』の30%はパーセント表記なので一見利益率を示しているかのように思ってしまいますが、これは利益率ではなくあくまで利益の額を示しています。問題文にもしっかりと『利益』と明記されていますよね。

30%の利益は単純に原価1,400円に30%をかけた金額になります。
30%の利益=1,400円×30%=420円
よって、定価は1,400円+420円=1,820円となります。

しかし、定価1,820円では売れないので1割引きで売ったということなので、現在の売値は次の通りになります。
割引価格=1,820円×1割=182円
よって、1割引きした現在の売値は次の通り。
現在の売値=1,820円-182円=1,638円
補足解答
分かり易く丁寧に解説しましたが、1割の値引きというのは定価の9割の値段に該当するので、下記のように求めることができます。
現在の売値=1,820円×9割=1,638円
計算はこちらの方が圧倒的に早いので、実際の試験のさいはこちらを利用できるようにしておいてください。
問題5の解答と解説
試験問題5の解答:ア
この問題を解くには以下の公式を頭に入れておく必要があります。

この問題を解くには、川の流れのスピードを考慮する必要があります。下るさいは川の流れが船の速度に加算されますが、上る場合は船のスピードを落とすことになります。
川の流れの速さを時速Mkm、求めたい船の速さを時速Vkmと仮定します。
下りは1時間かかるので、公式より次の式が成り立ちます。
速度=距離/時間
(V+M)=8/1
V+M=8 ・・・①
次に登りは2時間かかるので、公式より次の式が成り立ちます。
速度=距離/時間
(V-M)=8/2
V-M=4・・・②
①②より、求めたい船の速度を導きます。
V+M=8 ・・・①
V-M=4・・・②
2V=12
V=6
よって、船の速度は時速6km
公式の補足
公式は分数が含まれる『速度=距離/時間』ではなく『距離=速度×時間』で覚えたいという人もおられるかもしれませんが、『速度=距離/時間』の形で覚えておいた方が個人的には忘れにくいと思います。もし、忘れてしまった場合も簡単に思い出すことができます。車やバイクのスピードメーターを思い浮かべてみてください。
速度計の単位は『km/h』ですよね? そうです。これが速度を求める公式を表しています。
速度(km/h)=距離(km)/時間(h)
※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

