この問題は平成29年10月入校(試験実施日:平成29年8月25日)の大阪職業訓練短期過程の選考試験問題問3の解説です。特に難しい問題はありませんが、間違いやすい問題もあるのでこれらの過去問を繰り返し実施し、短時間かつ正確に解けるようにしておきましょう。
実際の試験の問題用紙は以下のページで確認することができます。
⇒平成29年10月入校 府立高等職業技術専門校 入校選考試験問題
問1、問3~問4に関しては以下のページに解説をまとめているので参考にして下さい。
問3 試験問題
下の図において、AB=36㎝、CD=45 ㎝、ABとCDとEFは平行である。以下の問いにア~オの中から1つ選び、記号で答えなさい。
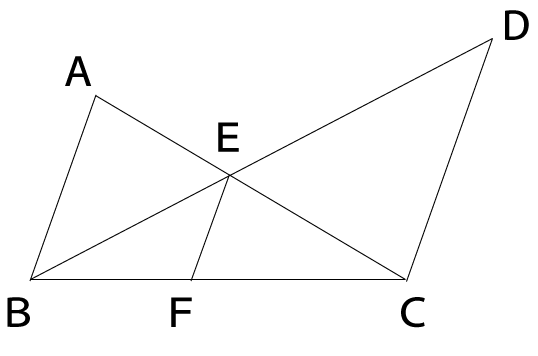
[問題1] BE:DEを求めなさい。
[解答群]
- 3:4
- 4:5
- 5:6
- 6:7
- 7:8
[問題2] △ABEと△CDEの面積比を求めなさい。
[解答群]
- 4:5
- 6:11
- 11:18
- 16:25
- 21:32
[問題3] EFの長さを求めなさい。
[解答群]
- 18㎝
- 20cm
- 22cm
- 24cm
- 26cm
解答と解説
解答と解説を記載していきます。
解き方が分からないという人を少しでも減らすためにできる限り分かり易く必要以上に細かく順を追って解説している部分がありますが、実際の試験時は丁寧に計算し過ぎると時間のロスに繋がるため、自分の分かるところは効率よく解答していくようにしてください。
問題1の解答と解説
試験問題1の解答:イ
まずは、問題文から分かっていることを図に書き込むと下図のようになります。
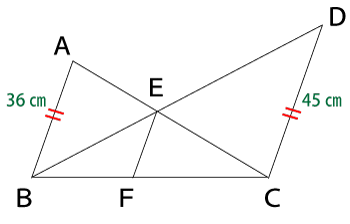
辺ABと辺CDが平行なので、次の式が成り立ちます。
∠AEB=∠CED
∠ABE=∠CDE
∠EAB=∠ECD
よって、三角形ABEと三角形CDEは3つの内角がそれぞれ等しいためこの二つの三角形は相似条件を満たしており、相似な三角形ということがわかります。
三角形の相似条件
- 2つの三角形の3組の辺の比がすべて等しい
- 2つの三角形の2組の辺の比とその間の角がそれぞれ等しい
- 2つの三角形の2組の角がそれぞれ等しい
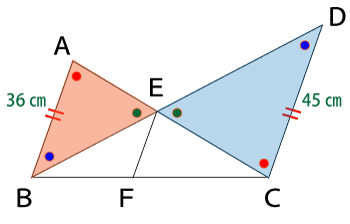
相似な三角形同士は、各辺の比も同じになるため求めたいBE:DEの比は以下のようにあらわすことができます。
BE:DE=AB:CD
BE:DE=36:45
BE:DE=4:5
よって、BE:DEの比は4:5
問題2の解答と解説
試験問題2の解答:エ
この問題を解くには相似比と面積比の関係を覚えておく必要があります。
2つの相似な三角形の相似比がa:bのとき、面積比は次のようになります。
相似比 a:b
面積比 a²:b²
この関係を覚えていればこの問題は簡単に解くことができます。相似比は問題1より4:5と分かっているので、面積比は以下のようになります。
面積比=4²:5²=16:25
問題3の解答と解説
試験問題3の解答:イ
三角形BCDと三角形BFEに着目します。
問題文より辺EFと辺CDは平行なので、二つの三角形の各内閣はすべて等しいため三角形BCDと三角形BFEもまた相似な三角形だと分かります。また、問題1の回答よりBE:DE=4:5と分かっています。
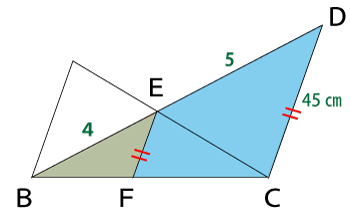
よって、次の関係式が成り立ちます。
BE:BD=EF:DC
4:(4+5)=EF:45
4:9=EF:45
9xEF=45x4
9EF=180
EF=20cm
※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

