大阪 職業訓練 試験問題 数学-問4(平成30年8月23日実施) 短期課程

問４ 試験問題

関数ｙ＝12X²・・・(1)のグラフと直線l が 2 点 A（－4，8）、B（2，2）で交わっている。以下の問いの答えとして正しいものをア～オの中から１つ選び、記号で答えなさい。

[問題1]　直線l の式を求めよ。

[問題2]　点 P が関数(1)の曲線上を A から B まで動く時、△ABP の面積が 9 になる時の点 P のx 座標の中で、 xが負の値をとる xの値を求めよ。

解答と解説

解答と解説を記載していきます。
解き方が分からないという人を少しでも減らすためにできる限り分かり易く必要以上に細かく順を追って解説している部分がありますが、実際の試験時は丁寧に計算し過ぎると時間のロスに繋がるため、自分の分かるところは効率よく解答していくようにしてください。

問題１の解答と解説

試験問題１の解答：エ

直線の式はｙ＝ａｘ+ｂで表すことができます。

直線ｌは2 点 A（－4，8）、B（2，2）を通るということなので、これを上の式に代入します。

ｙ＝ａｘ+ｂ
8＝-4ａ+ｂ ・・・①

ｙ＝ａｘ+ｂ
2＝2ａ+ｂ ・・・②

式①－②を行い直線の傾きａの値を求めていきます。

①－②
(8-2)＝(-4ａ+ｂ)-(2ａ+ｂ)
6＝-6ａ
ａ＝-1

このａの値を式①もしくは②へ代入し直線ｌの切片ｂを求めていきます。

2＝2ａ+ｂ ・・・②
2＝-2+ｂ
ｂ＝4

よって、直線ｌの式は次の通り。

ｙ＝-Ｘ+4

問題２の解答と解説

試験問題２の解答：-1-√3

短期課程の問題は中学卒業レベル扱いになっているため、本来の解き方であれば点Ｐを原点に移動し、△ABPをY軸で2等分し面積を合計する方法で求めるのですが、時間がかかる上、間違いやすいので高校で習う2点間の距離を求める公式と、直線と点の距離を求める公式を利用して解いていきます。

点Ｐは放物線上を動くため点ＰのＸ軸座標をｍとした場合、Ｙ座標はｍ²2となります。

点Ｐ(ｍ , ｍ²2)

公式より、点A(-4,8)と点B(2,2)の距離は次の通り。

点ABの距離＝√(2-(-4))²+(2-8)²
　　　　　＝√(2+4)²+(2-8)²
　　　　　＝√36+36
　　　　　＝√72
　　　　　＝6√2

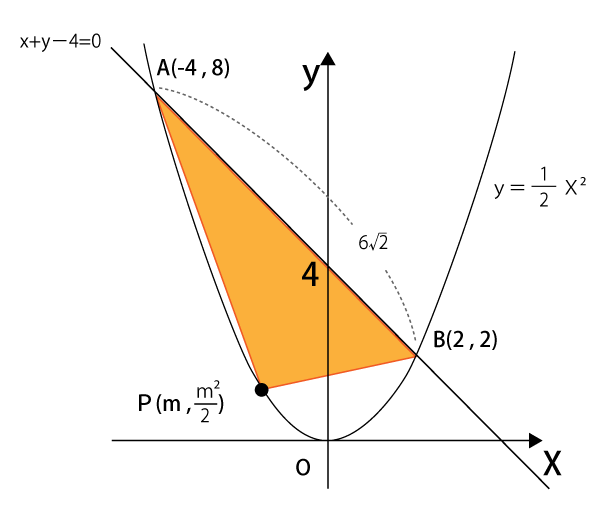
次に直線ABと点Pの距離を求めます。直線ABの式は問１より、ｙ＝-X+4 だと分かっています。この直線の式を公式の形式に変形すると、X+ｙ-4＝0となります。

直線ABと点Pの距離＝|m+m²/2-4|√1²+1²
　　　　　　　　＝|m+m²/2-4|√2
　　　　　　　　＝|m²+2m-8|2√2

また、点ＰのＸ座標が負の値をとるということから、ｍは-4＜ｍ＜0の範囲となります。ｍが-4＜ｍ＜0の範囲のとき、上記式の分子の絶対値内m²+2m-8は必ずマイナスとなります。|m²+2m-8|は絶対値なのでプラスに変換するために-1をかけ、絶対値を外します。

直線ABと点Pの距離＝-m²-2m+82√2

よって、三角形ABPの面積は設問より9と分かっているので以下の式が成り立ちます。

三角形ABPの面積＝底辺×高さ÷2
9＝6√2×-m²-2m+82√2×12

18＝3×(-m²-2m+8)
6＝-m²-2m+8
m²+2m-2=0

m=-2±√122
　＝-2±2√32
　＝-1±√3

mは負の値になるので、ｍ＝-1-√3

よって、△ABPの面積が9となり、かつ点PのX座標が負となる、X座標の値は-1-√3

※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。