次の(1)~(10)の計算をしなさい。
[問題1] -28-46=
[問題2] 70-7×6=
[問題3] 15÷3+4×3-5=
[問題4] 0.6×40=
[問題5]
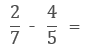
[問題6]
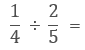
[問題7]
![]()
[問題8] 2a²b²×a²c³÷2abc²=
[問題9]

[問題10] 2次不等式 2X²+X-3<0 の解を求めなさい。
解答と解説
試験問題1の解答:-74
試験問題2の解答:28
試験問題3の解答:12
試験問題4の解答:24
試験問題5の解答:

試験問題6の解答:
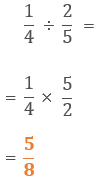
試験問題7の解答:
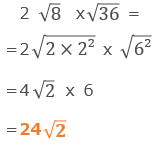
試験問題8の解答:
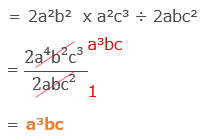
試験問題9の解答:

試験問題10の解答:
この問題は、因数分解ができることが必須となる。
2X²+X-3 < 0 を因数分解すると下記のようになる。
(2X+3)(X-1) < 0
2次方程式であれば、X=-3/2 、1 となるのだが、今回の問題は2次不等式です。Xの値ではなく、Xの取り得る範囲を求めないといけない。2次方程式のグラフを描いてみると分かり易いのだが、いちいちグラフを描いていると時間がたりなくなる。よって、下記の法則は覚えておいて欲しい。
(x-α)(x-β)<0のときはα<x<β (α<β)
(x-α)(x-β)>0のときはx<α、x<β (α<β)
よって、求める解答は、 -3/2 < X < 1 となる。

