平成28年度に埼玉県で実施された職業訓練(短期コース)の選考試験で出題された試験問題と、その解答と解説です。 本ページでは数学問題の問題3(正式なテスト用紙上では設問7)のみ記載しています。その他の問題に関しては、以下のページを参照してください。
埼玉 職業訓練 試験問題[短期] 数学-問1(平成28年入校生)
埼玉 職業訓練 試験問題[短期] 数学-問2(平成28年入校生)
埼玉 職業訓練 試験問題[短期] 数学-問4(平成28年入校生)
試験問題 設問3
7. 次の問いに答えなさい。
[問題1]
「訓」「練」と書かれた同じ大きさの2枚のメダルが、北向きに並んで2枚置いてある。「訓」メダルを、もう1枚の「練」メダルの周囲に沿ってすべらないように矢印の方向に回転させる。図の点線の位置に来たときの「訓」メダルの向きを図中の方位で記述しなさい。
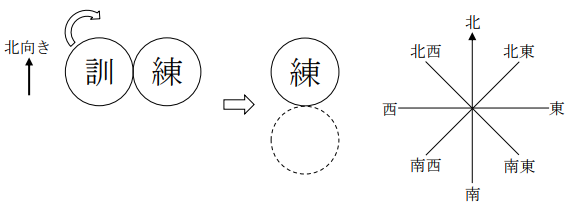
[問題2]
下図で、AB=4cm、AC=4cm、DC=2cm のとき、BDの長さを求めなさい。
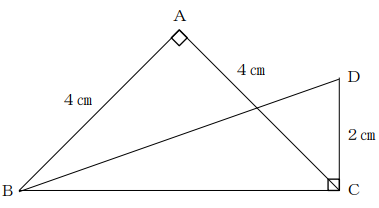
解答と解説
試験問題1の解答:
「訓」メダルと「練」メダルの接点は下図のように「練」のメダルの周囲270°分を移動します。
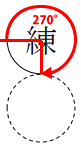
この時、「訓」のメダル側の接点も同様に下図のように270°分移動します。
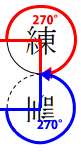
よって、「訓」メダルの向きは、南向きだと分かります。
解答:南
試験問題2の解答:
この問題を解くにあたり、知っておかなければならないのが下の「三平方の定理」です。

問題の三角形ABCと三角形BCDはいずれも直角三角形なのでこの三平方の定理で各辺の長さを求めることができます。
三角形ABCについて考える
三角形ABCの辺の長さで分かっていないのは辺BCの長さ。三平方の定理で求めると下記のようになります。
BC²=4²+4²
BC²=16+16
BC²=32
BC=√32
BC=√16√2
BC=4√2
※補足
直角二等辺三角形の場合、各辺の長さは「1:1:√2」となります。これを頭に入れておくとより早くこの問題を解くことができます。
三角形BCDについて考える
三角形BCDの辺BCは4√2だと分かったので、わかっていないのは求めたい辺BDの長さのみ。三平方の定理を使うと下記の様に解くことができます。
BD²=DC²+BC²
BD²=(4√2)²+2²
BD²=(16×2)+4
BD²=32+4
BD²=36
BD=√36
BD=6
よって、辺BDの長さは6cm
解答:6cm

