平成28年度に埼玉県で実施された職業訓練(短期コース)の選考試験で出題された試験問題と、その解答と解説です。 本ページでは数学問題の問題4(正式なテスト用紙上では設問8)のみ記載しています。その他の問題に関しては、以下のページを参照してください。
埼玉 職業訓練 試験問題[短期] 数学-問1(平成28年入校生)
埼玉 職業訓練 試験問題[短期] 数学-問2(平成28年入校生)
埼玉 職業訓練 試験問題[短期] 数学-問3(平成28年入校生)
試験問題 設問4
8. 次の問いに答えなさい。
[問題1]
下図左の展開図のサイコロを2つ組み立てて、下図右のように並べた。このときAの目はいくつか。ただし、2つのサイコロが接している面の和は7とする。
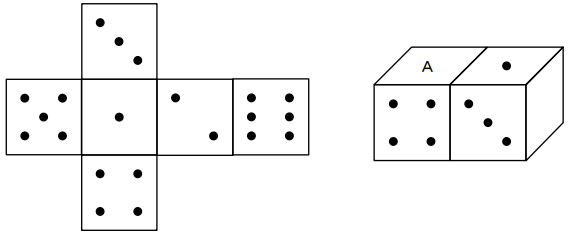
[問題2]
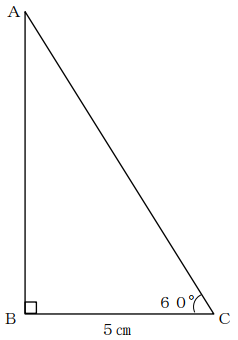
下図のような、BC=5㎝、∠C=60°、∠B=90°の直角三角形がある。この三角形を辺ABを軸として1回転させてできる立体の表面積を求めなさい。ただし円周率をπとする。
解答と解説
試験問題1の解答:
サイコロ②について考える
まず、下図のB面に何の数字がくるか考える。展開図より、1の目と3の目の両方の面に接する面は「5」か「2」になるが、並べられたサイコロ②の向きよりBには「5」がくることが分かる。よって、サイコロ①とサイコロ②が接する方のサイコロ②の面は「2」ということになります。
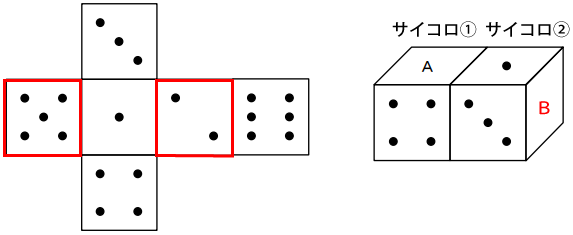
サイコロ①について考える
2つのサイコロが接している面の和は7ということなので、サイコロ①とサイコロ②が接するサイコロ①の面は「5」だと分かります。サイコロ①の4の目と5の目両方の面に接する面は「1」と「6」になります。並べられたサイコロ①の向きよりAの面にくるのは「6」だと分かります。
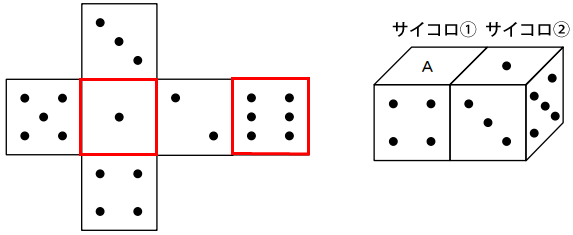
解答:6
試験問題2の解答:
この問題を解く上で知っておきたいのが下図の直角三角形の辺の長さの特徴です。
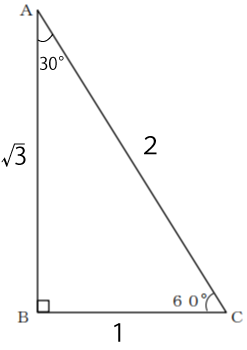
内角が90°、60°、30°となる直角三角形の場合、各辺の長さの比が上図のように
1:2:√3
となります。よって、今回の問題の直角二等辺三角形の場合、各辺の長さは下図のようになります。
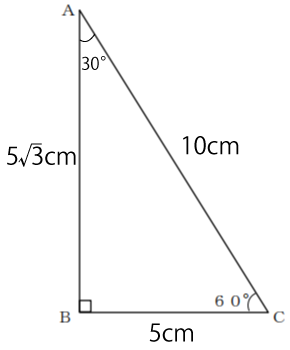
ここで円錐の表面積を求める公式を知っていればこの問題は簡単に解けるのですが、公式を覚えている人は少ないと思います。よって、ここでは公式を使わずに解説します。
三角形の辺ABを軸にして1回転回すと下図のような円錐ができます。
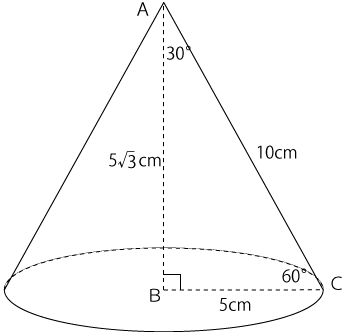
この円錐を展開すると下図のような図形になります。
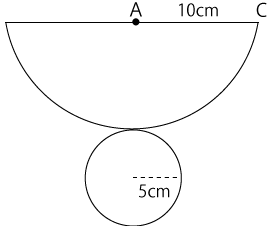
求めなければならないのは、円錐の側面にあたる扇型の面積と円錐の底面にあたる円の面積です。この2つの合計面積が円錐の表面積となります。
円の面積
円錐の底面にあたる円の面積を求めます。半径が5cmなので、円の面積は次の通り。
円の面積=半径x半径xπ
=5x5xπ
=25π ・・・(1)
扇型の面積
辺ACを半径とした円の面積は次の通り。
円の面積=半径x半径xπ
=10x10xπ
100π ・・・(2)
辺ACを半径とした円の円周は次の通り。
円の円周=直径xπ
=(10+10)xπ
=20π ・・・(3)
ここで底面の半径5cmの円の円周も求めます。
底面の円の円周=直径xπ
=(5+5)xπ
=10π ・・・(4)
この底面の円の円周の長さは、下図の赤線部分に相当します。
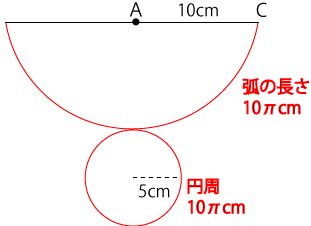
辺ACを半径とした円の円周は(3)より、20πと分かっているので、弧の長さが10πということは、この扇型は辺ACを半径とした円の1/2(10π/20π)だということが分かります。よって、扇型の面積も辺ACを半径とした円の面積の1/2になります。
辺ACを半径とした円の面積は(2)より、100πだと分かっているので扇型の面積は次の通りになります。
扇型の面積=100π/2
=50π ・・・(5)
円錐の表面積
円錐の表面積は、円錐の側面部分にあたる扇型の面積(5)と円錐の底面にあたる円の面積(1)の合計なので次の通りになります。
円錐の表面積=25π+50π
=75π
解答:75π

