埼玉職業訓練試験問題[短期] 数学-問3(平成29年入校生)

平成29年度に埼玉県で実施された職業訓練(短期コース)の選考試験で出題された試験問題と、その解答と解説です。本ページでは数学問題の問題3(正式なテスト用紙上では設問8)のみ記載しています。その他の問題に関しては、以下のページを参照してください。

８. 次の（１）、（２）の問いに答えなさい。

[問題1]
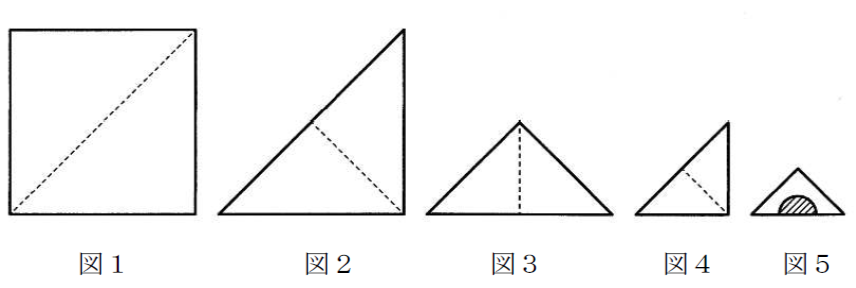
下図の正方形の紙を図１から図４の順に点線に沿って４回折った。図５の大きさになったところで斜線部分の半円を切り取った。もとの正方形に開いたとき完全な円になっている穴は何個できているか。次の１から５のうち番号で答えなさい。

[問題2]
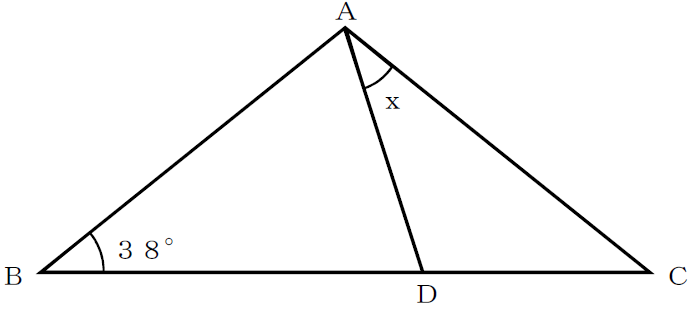
下図のように、ＡＢ＝ＡＣ、∠ＡＢＣ＝３８°の二等辺三角形の辺ＢＣ上に、ＢＡ＝ＢＤとなる点Ｄをとるとき、ｘの角度は何度となるか求めなさい。

試験問題１の解答：
一番簡単で確実な方法は、図5から図4→図3→図2→図1と展開しながら斜線部分を問題用紙に塗りつぶして確認していく方法です。

図5から図4へ展開

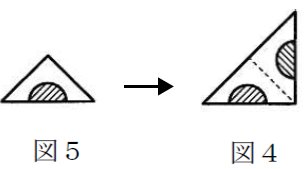
図4から図3へ展開

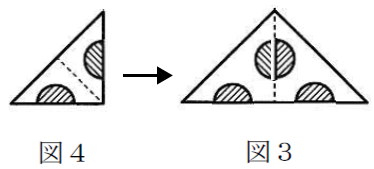
図3から図2へ展開

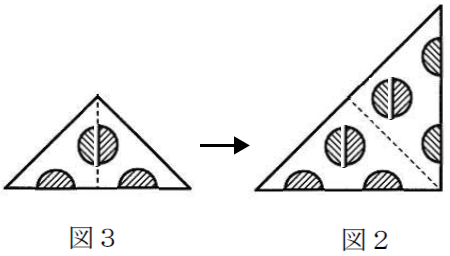
図2から図1へ展開

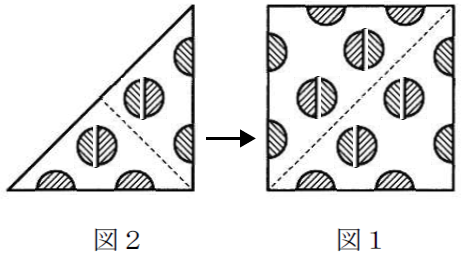
図より完全な円は4個と分かります。よって、解答は2番。

解答：2

試験問題２の解答：
下図の①～④の順で角度を求めていきます。

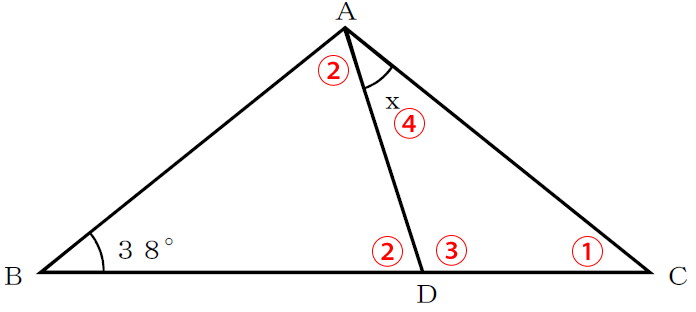
三角形ＡＢＣの辺ＡＢ＝ＡＣということなので、三角形ＡＢＣは二等辺三角形ということになります。よって、∠ＡＣＢ＝∠ＡＢＣだとわかるので、∠ＡＣＢ＝38°となります。

①∠ＡＣＢ＝38°

更に辺ＢＡ＝辺ＢＤということなので、三角形ＡＢＤも二等辺三角形ということになります。三角形の内角の和は180°なので、②の角度は次の通り。

∠ＢＡＤ＋∠ＢＤＡ＋38°＝180°
∠ＢＡＤ＋∠ＢＤＡ＝142°

三角形ＡＢＤは二等辺三角形なので∠ＢＡＤ＝∠ＢＤＡとなります。よって、②の角度は次の通り。

②∠ＢＡＤ＝∠ＢＤＡ＝142÷2＝71°

「∠ＢＤＡ＝71°」なので∠ＡＤＣは次の通り。

③∠ＡＤＣ＝180-71＝109°

三角形の内角の和は180°なので、角①+③+④は180°となります。よって、求めたい各④のＸは次の通り。

角④＝180-38-109＝33°

解答：Ｘ＝33°

関連記事