平成29年度に埼玉県で実施された職業訓練(短期コース)の選考試験で出題された試験問題と、その解答と解説です。 本ページでは数学問題の問題4(正式なテスト用紙上では設問9)のみ記載しています。その他の問題に関しては、以下のページを参照してください。
埼玉 職業訓練 試験問題[短期] 数学-問1(平成29年入校生)
埼玉 職業訓練 試験問題[短期] 数学-問2(平成29年入校生)
埼玉 職業訓練 試験問題[短期] 数学-問3(平成29年入校生)
試験問題 設問4
9. 次の(1)、(2)の問いに答えなさい。
[問題1]
下図は立方体の展開図で、AからHはのりしろを示している。この展開図を組み立てたとき、重なるのりしろはどれか。次の1から5のうち番号で答えなさい。
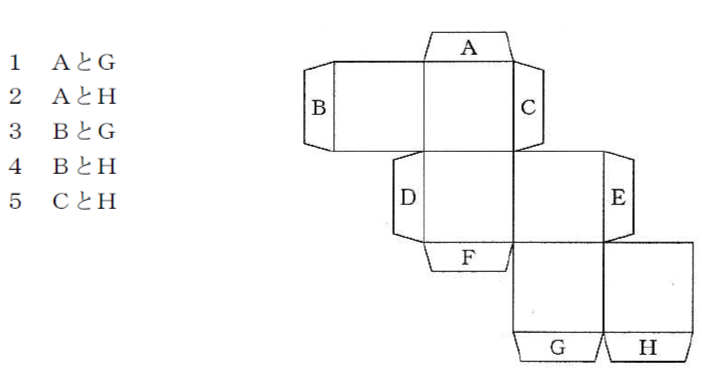
[問題2]
下図は1辺の長さが8cmの正方形の中に、直径が8cmの半円が入っている図形である。斜線の部分の面積は何cm2となるか求めなさい。ただし、円周率はπとする。
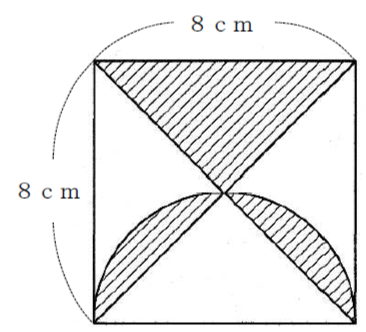
解答と解説
試験問題1の解答:
下図ののりしろCDEFは、赤文字CDEFの場所に重なるのは直ぐに分かると思います。これらは他のアルファベットののりしろに重なることはないので、解答群からCDEFが絡むものは除外できます。解答5は除外。
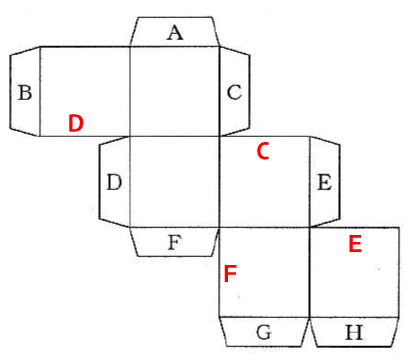
残りは頭の中で図を組み立てつつ考えるしかないのですが、下図のように各面が組み立てた時にどこに位置するかを問題用紙に記入しつつ考えると分かりやすいかもしれません。
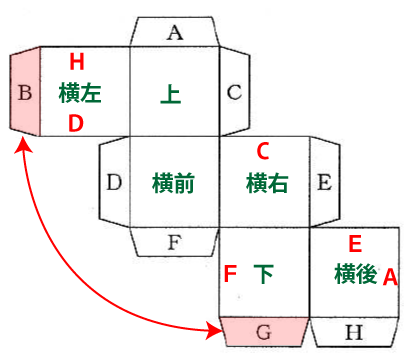
解答は、BとGの3番。
解答:3
試験問題2の解答:
斜線部分の合計面積を求めるのは次の流れで行います。
- 三角形の面積を求める
- 直径8cmの半円の面積を求める
- 直径8cmの半円の面積から三角形の面積を引く
- 1.と3.の面積を合計する
三角形の面積を求める
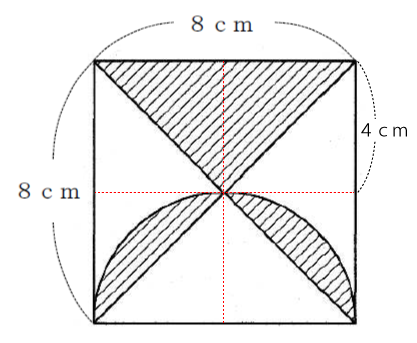
斜線部分の三角形の底辺の長さは8cm、高さは4cmなので斜線部分の三角形の面積は次の通りになります。
三角形の面積=8x4÷2
=16cm² ・・・(1)
直径8cmの半円の面積を求める
円の面積を求める公式
円の面積=半径x半径xπ
よって、直径8cmの円の面積は次の通り。
円の面積=4x4xπ
=16π
求めたいのは直径8cmの円の半円の面積なので、その面積は次の通り。
半円の面積=16π÷2
=8π ・・・(2)
直径8cmの半円の面積から三角形の面積を引く
半円の面積(2)から三角形の面積(1)を引いた面積が円の斜線部分(下図①)の面積になります。
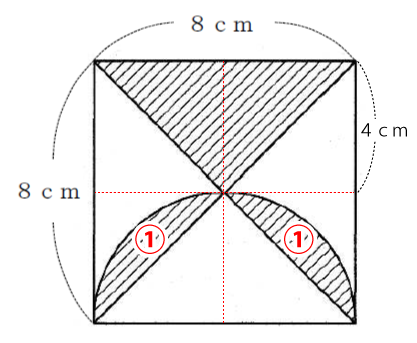
半円斜線部分面積=8π-16 ・・・(3)
斜線部分の合計をするく
三角形の面積(1)と半円の斜線部分の面積(3)の合計が今回求めたい面積になります。よって、その面積は次の通り。
16+(8π-16)=8π
解答:8π cm²

