埼玉 職業訓練 試験問題 数学-問6(平成30年度生 二年・一年コース)

問６ 試験問題

次の（１）から（１０）の計算をしなさい。ただし、分数で約分のできる場合は最後まで約分すること。

（１）－５６＋１９＝

（２）２４－６×７＝

（３）５×３＋４８÷６－１８＝

（４）４２÷０．７＝

（５）－3/4＋11/12＝

（６）4/7÷2/3＝

（７）√18×√50＝

（８）３ａ²ｂ²ｃ×４ａ²ｂ²÷２ａｂ²ｃ＝

（９）Ｘ＝－４、Ｙ＝２のとき、３(Ｘ²＋3Ｙ)－1/2(Ｘ＋3Ｙ²)＝

（１０）２次不等式Ｘ²－4Ｘ－12≦0の解を求めなさい。

解答と解説

試験問題１の解答：－37

試験問題２の解答：－18
掛け算の計算が足し算よりも優先。
24-6×7
＝24-42
＝-18

試験問題３の解答：5
掛け算と割り算の計算が足し算と引き算より優先。
5×3+48÷6-18
＝(5×3)+(48÷6)-18
＝15+8-18
＝5

試験問題４の解答：60
42÷0.7
＝60

試験問題５の解答：1/6
-3/4+11/12
＝-9/12+11/12
＝2/12
＝1/6

試験問題６の解答：6/7
4/7÷2/3
＝4/7×3/2
＝6/7

試験問題７の解答：30
√18×√50
＝√900
＝√30×30
＝30

試験問題８の解答：6ａ³ｂ²
3ａ²ｂ²ｃ×4ａ²ｂ²÷2ａｂ²ｃ
＝12ａ⁴ｂ⁴ｃ÷2ａｂ²ｃ
＝6ａ³ｂ²

試験問題９の解答：62
3(Ｘ²＋3Ｙ)－1/2(Ｘ＋3Ｙ²)にＸ＝－４、Ｙ＝２を代入して計算していきます。

3(Ｘ²＋3Ｙ)－1/2(Ｘ＋3Ｙ²)
＝3((-4)²＋3×2)－1/2(-4＋3×(2)²)
＝3(16+6)-1/2(-4+3×4)
＝3×22-1/2(-4+12)
＝66-1/2×8
＝66-4
＝62

試験問題１０の解答：－2≦Ｘ≦6
Ｘ²－4Ｘ－12≦0
(Ｘ－6)(Ｘ＋2)≦0
－2≦Ｘ≦6

Ｘの値が－2と6だということは分かるが、なぜ解がＸ≦－2、6≦Ｘではなく－2≦Ｘ≦6という範囲になるのか分からないという人は以下のグラフを頭に入れておけば簡単に分かるようになります。

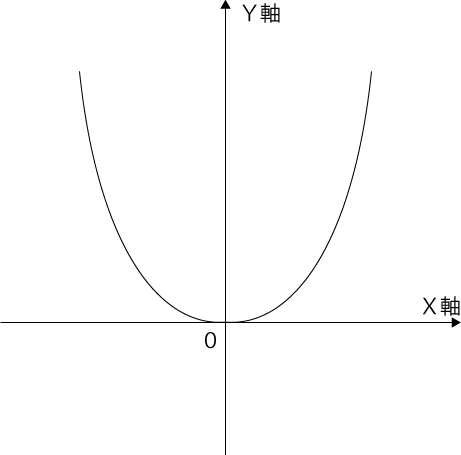
二次方程式『Ｙ＝Ｘ²＋aＸ＋b』というグラフは、下図のような放物線のグラフになります。

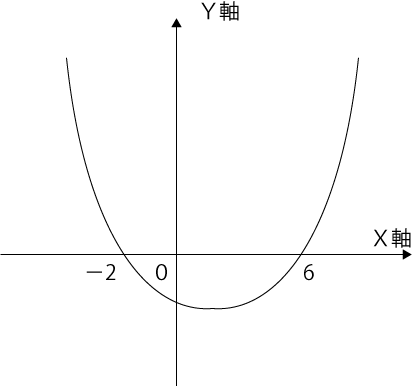
今回の問題では、Ｘが－2と6を通ると分かったのでＸ²－4Ｘ－12のグラフは下図のようになります。

さらに今回の問題では、Ｘ²－4Ｘ－12≦0のようにＹの値が0よりも小さい範囲を示しているのでグラフの下図の部分に該当します。

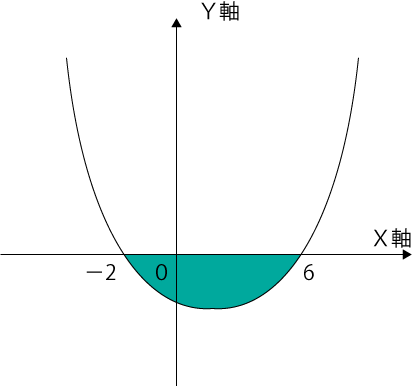
よって、この緑色の部分を示すＸの範囲は－2≦Ｘ≦6となります。
逆に今回の問題が『Ｘ²－4Ｘ－12≧0』だった場合は、Ｙはプラス領域を示すので下図の範囲になります。

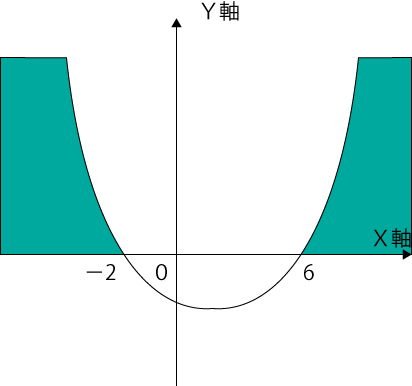
よって、この場合の回答は、『Ｘ≦－2、6≦Ｘ』となります。

計算の補足事項

足し算や引き算、掛け算、割り算の計算の優先順位を間違えると誤った解答になってしまうので注意してください。計算の優先順位について知りたい方は下記のページ(外部サイト)で詳しく解説しているので宜しければ参考にしてください。

※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。