この問題は平成24年4月入校の東京都立職業能力開発センター入校選考試験問題の問２と問３の解答と解説です。

問１、問４～問６に関しては以下のページに解説をまとめているので参考にして下さい。

実際の試験の問題用紙は以下のページで確認することができます。

⇒都立職業能力開発センター入校選考試験問題(平成24年04月生)

■目次

  1. 試験問題２
  2. 試験問題３

問２ 試験問題

ある自動車が毎秒15ｍの一定速度で２時間40分走り続けたとき、その走行距離は何kmになりますか。

解答と解説

試験問題２の解答：144ｋｍ

この問題を解くには距離と速度と時間の公式を知っている必要があります。

速度と時間と距離の関係

さらにこの問題は若干のひっかけがあるので注意が必要です。

そのひっかけとは単位です。問題文は『メートルとキロメートル』、『時間と分と秒』と単位がバラバラになっています。計算するさいはどの単位でも構いませんが単位を統一して計算するようにしてください。

今回は、計算時はメートルと秒に統一して計算します。ただし、解答は『ｋｍ』で求められているため、最後にｋｍに変換していきます。

問題は走行距離を求めるので公式を以下のように変形して計算します。

速度＝距離÷時間
↓

距離＝速度×時間

速度＝15ｍ/秒
時間＝2時間40分＝9600秒

距離＝15×9600
　　＝144000ｍ
　　＝144ｋｍ

よって、走行距離は144ｋｍ

問３ 試験問題

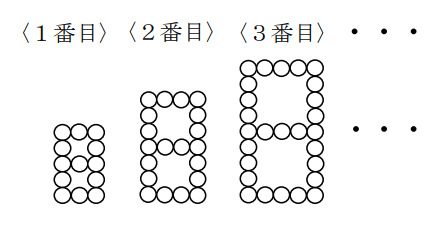
碁石を使って図の１番目、２番目、３番目、･･･のように、碁石の数を増やして正方形を２つ合わせた図形をつくります。このとき、13番目の図形をつくるのに必要な碁石は何個ですか。

碁石を並べた図形

解答と解説

試験問題３の解答：97個

1番目の碁石の数は13個、2番目は20個、3番目は27個と{13、20、27・・・}と増えていっています。よって、Ｎ番目の碁石の数は次のようにあらわすことができます。

(初期値)＋(増分幅)
13＋(Ｎ－1)×7
＝13＋7Ｎ－7
＝6＋7Ｎ

よって、13番目の碁石の数は次の通り。

6＋7Ｎ
＝6＋7×13
＝6＋91
＝97個

※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。