この問題は平成24年4月入校の東京都立職業能力開発センター入校選考試験問題の問６の解答と解説です。

問１～問５に関しては以下のページに解説をまとめているので参考にして下さい。

実際の試験の問題用紙は以下のページで確認することができます。

⇒都立職業能力開発センター入校選考試験問題(平成24年04月生)

問題を解くのに必要な知識

  • 三角形の面積を求める公式

問６ 試験問題

図において、Ｏは原点、点Ａ、Ｂの座標はそれぞれ（－４，０）、（３，７）です。また、点Ｃのy 座標は正です。⊿ＡＯＢと⊿ＣＯＢの面積が等しいとき，点Ｃのy 座標を求めなさい。

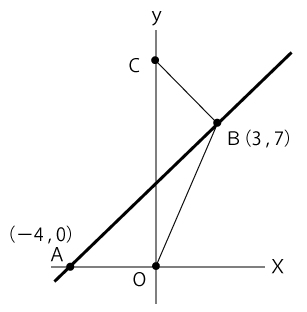
2点を通る直線

解答と解説

試験問題６の解答：28/3

まずは、△ＡＯＢの面積を求めていきます。
△ＡＯＢの底辺はＯＡの長さ4、高さは点ＢからＸ軸に垂線を下ろした線の長さなので7だと分かります。

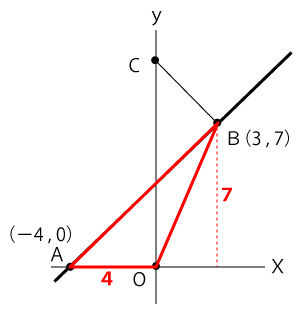
三角形の面積

よって、△ＡＯＢの面積は次の通り。

△ＡＯＢの面積＝4×7÷2
　　　　　　　＝14・・・①

次に△ＣＯＢの面積をもとめていきます。
△ＣＯＢの底辺をＣＯとすると、その長さはＣ点のｙ座標になるので仮にｙとしておきます。さらに高さは点Ｂからｙ軸に垂線を下ろした線になるので、ＢのＸ軸の値である3となります。

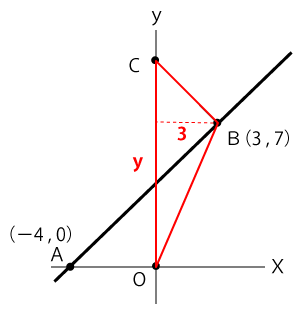
三角形の面積

よって、△ＣＯＢの面積は次のようにあらわすことができます。

△ＣＯＢの面積＝ｙ×3÷2
　　　　　　　＝3ｙ/2

問題文より△ＣＯＢの面積と△ＡＯＢの面積は等しく、さらに△ＡＯＢの面積は①より14だとわかっています。よって、以下の式が成り立ちます。

3ｙ/2＝14

この式を解くと点Ｃのｙ座標が求まります。

3ｙ/2＝14
3ｙ＝28
ｙ＝28/3

よって、Ｃ点のｙ座標は28/3

※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。