東京 職業訓練 試験問題[学力検査] 数学-問4,問5,問6(平成27年4月生)

問４ 試験問題

下のような正八角形ＡＢＣＤＥＦＧＨがあります。この８個の頂点から３個の頂点を選び、直角三角形をつくります。このとき，直角三角形は何通りありますか。

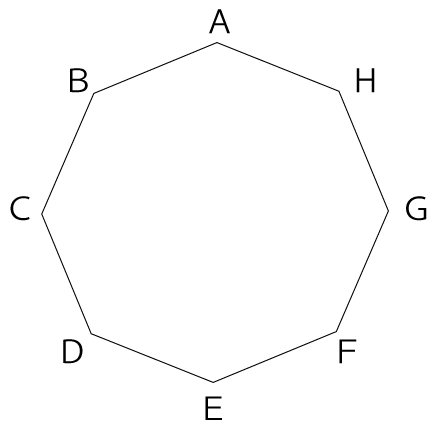
以下は解答と解説です。解答、解説を見る前にまずは自分自身でチャレンジしてみてください。

解答と解説

試験問題４の解答：24通り

この問題は力技で一つずつ洗い出しても解けますが、数え漏れをしてしまう可能性があるだけではなく時間もかかってしまいます。実は以下の点を知っていればこの問題は簡単に解くことができます。

今回の問題は正八角形なので円に内接することができ、さらに各頂点とその対角を結んだ線は円の中心を通ります。

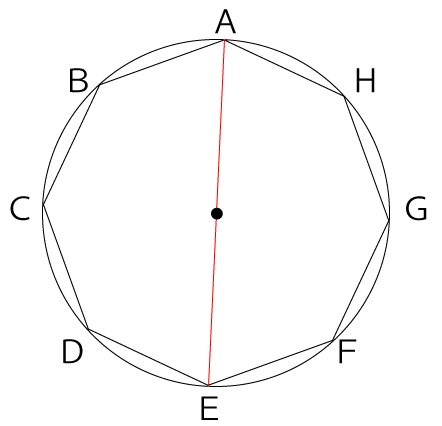
上図のように点Ａとその対角Ｅを結ぶとＡＥは円の中心を通ります。
次に三角形を作るために点ＡＥとそれ以外の点ＢＣＤＦＧＨと結ぶとどこと結んでも直角三角形ができます。

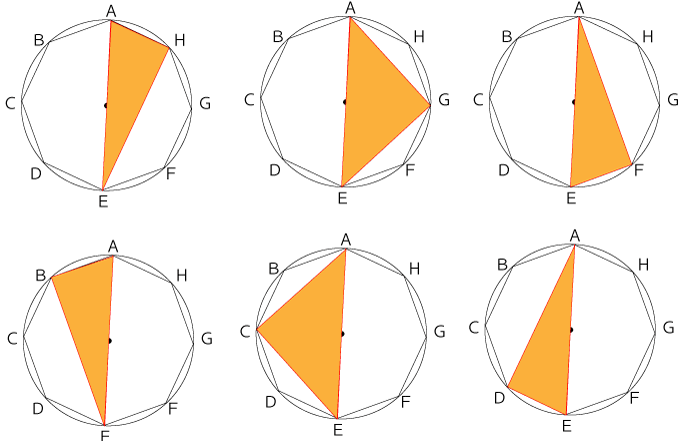
上図のように円の中心を通る一本の線ＡＥに対して6つの直角三角形ができます。

円の中心を通る中心線はＡＥ、ＨＤ、ＧＣ、ＦＢの全部で4本作れ、中心線1本に対して6つの直角三角形ができるので、直角三角形は全部で以下の通りだけつくれることになります。

直角三角形の数＝4×6
　　　　　　　＝24通り

よって、正八角形の頂点を3ヵ所選んでできる直角三角形の数は全部で24通り

問５ 試験問題

横軸をＸ、縦軸をＹとする座標があります。このとき、２点（－４,６）、（２,０）を通る直線の方程式を求めなさい。

以下は解答と解説です。解答、解説を見る前にまずは自分自身でチャレンジしてみてください。

解答と解説

試験問題５の解答：ｙ＝－Ｘ＋２

この問題を解くには直線の方程式を知っている必要があります。

直線の方程式

ｙ＝ａＸ＋ｂ

直線は、２点（－４,６）、（２,０）を通るということなので、それぞれの座標値を直線の式に代入し、傾きａと切片ｂを求めていきます。

点（－４,６）を通るので、直線の式にＸ＝－4、ｙ＝6を代入します。
ｙ＝ａＸ＋ｂ
6＝－4ａ＋ｂ・・・①

さらに点（２,０）を通るので、直線の式にＸ＝2、ｙ＝0を代入します。
ｙ＝ａＸ＋ｂ
0＝2ａ+ｂ
ｂ＝－2ａ・・・②

①式に②を代入します。
6＝－4ａ＋ｂ
6＝－4ａ＋(－2ａ)
6＝－6ａ
ａ＝－1

ａの値が分かったので式①もしくは式②にａの値を代入しｂの値を求めます。式②に代入した方が簡単ですね。

ｂ＝－2ａ・・・②
ｂ＝－2×(－1)
　＝2

よって、直線の方程式は次の通り。
ｙ＝ａＸ＋ｂ

ｙ＝－Ｘ＋２

問６ 試験問題

3√7/2 ＜ ａ ＜ 2√5 を満たす整数ａを求めなさい。

以下は解答と解説です。解答、解説を見る前にまずは自分自身でチャレンジしてみてください。

解答と解説

試験問題６の解答：ａ＝4

『√7＝2.6457…』『√5＝2.236…』ということを知っていれば簡単に解けますが、覚えている人はそうそういないですよね？

とは言え、ルートのままでは整数値が分からないのでまずはルートを外すためにすべてを2乗します。

(3√7/4)² ＜ ａ² ＜ (2√5)²
63/4 ＜ ａ² ＜ 20
15.75 ＜ ａ² ＜ 20

2乗した値が15.75から20の間に入るような整数ａを考えると、4だとわかります。

よって、不等式を満たす整数ａは4

※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。