この問題は平成31年4月入校の東京都立職業能力開発センター入校選考試験問題の問5の解答と解説です。
問1~問4、問6に関しては以下のページに解説をまとめているので参考にして下さい。
- 東京 職業訓練 試験問題[学力検査] 数学-問1(平成30年04月生)
- 東京 職業訓練 試験問題[学力検査] 数学-問2(平成30年04月生)
- 東京 職業訓練 試験問題[学力検査] 数学-問3(平成30年04月生)
- 東京 職業訓練 試験問題[学力検査] 数学-問4(平成30年04月生)
- 東京 職業訓練 試験問題[学力検査] 数学-問6(平成30年04月生)
実際の試験の問題用紙は以下のページで確認することができます。
問5 試験問題
1から12までの数が書いてある正十二面体のさいころがあります。これを投げるとき、上面が2の倍数でも3の倍数でもない数になる確率を分数で求めなさい。
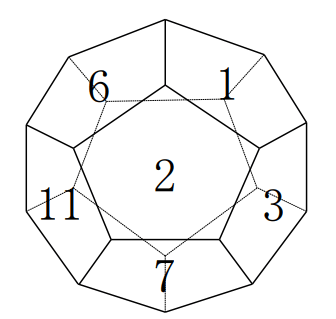
以下は解答と解説ですが、解答・解説を見る前にまずは自分自身でしっかりと考えるようにしてくださいね。
解答と解説
試験問題5の解答:13
サイコロの数字は1~12まであるので、出る目は全部で12通りあることになります。
次に1~12の数字の内、、2の倍数でも3の倍数でもない数を洗い出します。12種類しかないので1つ1つ確認して出していってください。
すると、以下の4つの数字が出てきます。
1、5、7、11
よって、2の倍数でも3の倍数でもない数は全12通り中、4通りあることになります。
従って、この4通りが出る確率は、412=13
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

