次の問に答えなさい。
[問題1] 家族4人で遊園地に行きました。大人一人の入園料が3,750円で子供一人の入園料は大人一人の入園料の3分の1でした。全員の入園料の合計が10,000円になるとき、大人の人数は何人ですか。ただし、消費税は考えないものとします。
[問題2] 濃度7％の食塩水500gに、濃度のわからない食塩水200gを加えたところ、濃度9％の食塩水ができました。このとき、加えた食塩水の濃度は何％ですか。
[問題3] 1から9までの整数が1つずつ書かれたカードが9枚あります。これらのカードから2枚引いて2桁の整数を作るとき、奇数は全部で何通りできますか。
[問題4] 自宅から学校までの2kmの道のりを、最初は毎分60m、途中からは毎分80mの速さで歩きます。自宅を出て30分以内に学校へ到着するためには毎分60mで歩く距離を何m以内にすればよいですか。
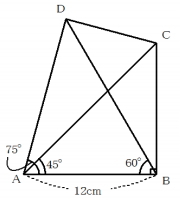
[問題5] 図のような四角形ＡＢＣＤがあります。この四角形の対角線をＡＣ、ＢＤとします。ＡＢ＝12cm、∠ＤＡＢ＝75°、∠ＣＡＢ＝45°、∠ＤＢＡ＝60°、∠ＡＢＣ＝90°のとき、ＤＣの長さは何cmですか。
解答と解説
試験問題１の解答：
求めたい大人の人数をＸと仮定します。家族の人数は4人なので、子供の人数は次のように表すことができます。
大人の人数＝Ｘ
子供の人数＝4－Ｘ
大人一人の入園料が3,750円で、子供の入園料が大人一人の1/3という事なので次の通り。
大人一人の入園料＝3,750円
子供一人の入園料＝3,750円×(1/3)＝1,250円
全員の入園合計量が10,000円ということなので次の式が成り立ちます。
全員の入園合計量＝(大人の人数)×(大人の入園料)＋(子供の人数)×(子供の入園料)
10000＝Ｘ × 3750 ＋ (4－Ｘ) × 1250
10000＝3750Ｘ ＋ 5000 － 1250Ｘ
3750Ｘ － 1250Ｘ ＝ 10000 － 5000
2500Ｘ＝5000
Ｘ＝2
解答：2人
試験問題２の解答：
食塩水の濃度の問題はよく出題されるので下記の公式は覚えておきましょう。
濃度(％) ＝ 食塩の量 ÷ 食塩水の量
『濃度7％の食塩水500g』と、『濃度のわからない食塩水200g』、さらにこの2種類を混合した『濃度9％の食塩水』の前部で3種類の食塩水があります。それぞれ1つずつ見ていきたいと思います。
◎濃度7％の食塩水500g
濃度が7％、食塩水の量が500gなので、食塩の量は、公式より次の通りになる。
濃度(％) ＝ 食塩の量 ÷ 食塩水の量
0.07 ＝ 食塩の量 ÷ 500
食塩の量 ＝ 500 × 0.07 ＝ 35g
よって、この食塩水は、
濃度： 0.07 (7％)
食塩の量： 35g
食塩水の量： 500g
◎濃度のわからない食塩水200g
濃度をＸと仮定すると、食塩の量は、公式より次の通りになる。
濃度(％) ＝ 食塩の量 ÷ 食塩水の量
Ｘ ＝ 食塩の量 ÷ 200
食塩の量 ＝ 200 × Ｘ ＝ 200Ｘg
よって、この食塩水は、
濃度： Ｘ
食塩の量： 200Ｘg
食塩水の量： 200g
◎濃度9％の食塩水
濃度9％、食塩水の量は、『濃度7％の食塩水500g』と、『濃度のわからない食塩水200g』の混合水なので700gになる。食塩の量は公式より次の通り。
濃度(％) ＝ 食塩の量 ÷ 食塩水の量
0.09 ＝ 食塩の量 ÷ 700
食塩の量 ＝ 700 × 0.09 ＝ 63
よって、この食塩水は、
濃度： 0.09 (9％)
食塩の量： 63g
食塩水の量： 700g
ここで、混合させた2種類の食塩水の食塩の合計量は63gとわかりました。2種類の内の一方の食塩の量は、35gと分かっているので、もう一方の食塩の量は、28g(63－35)となります。
そして、前述ではその食塩の量は、200Ｘとしていたので次の式が成り立ちます。
200Ｘ＝28
Ｘ＝0.14
よって、求めたい加えた食塩水の濃度は14％
解答：14％
試験問題３の解答：
2桁の整数が奇数となるには、一桁目の数字が奇数になる必要があります。よって、一桁目と二桁目の組合せ数は次の通り。
一桁目
1から9までの整数で奇数となるのは、1、3、5、7、9の5通り
二桁目
二桁目は、奇数、偶数に関係がないので1から9までの9つの数値を取り得ることができます。しかし、一桁目で使った数字は二桁目では使えないので、実質二桁目は8種類の数字の中から選ぶ必要があります。
よって、二桁目の組み合わせ数は、8通り
一桁目の取り得る組み合わせ数が5通り、二桁目が8通りなので、二桁の整数で奇数ができる組み合わせ数は次の通り。
5 × 8 ＝ 40通り
解答：40通り
試験問題４の解答：
速度、距離、時間を求める公式を使用する問題は頻繁に出題されるので必ず覚えておきましょう。
速度 ＝ 距離 ÷ 時間
速度、距離、時間を求める問題は毎回、単位のひっかけがあるので注意が必要です。
距離を表す単位が『km』に対して、速度を表す単位が『m/分』とメートルが使用されています。単位を統一して計算しないと全くことなた解答になってしまいます。この問題では、解答が『ｍ』で求められているのでまずは、単位を『ｍ』に統一したいと思います。
自宅から学校までの距離＝2㎞＝2000m
次に、求めたい毎分60mで歩く距離をＬ、そのときの歩いた時間をＭと仮定して計算します。まずは、分かっている点の整理。
自宅から学校までの距離： 2000(メートル)
自宅から学校までの時間： 30(分)
毎分60mで歩く距離： Ｌ(メートル)
毎分60mで歩く時間： Ｍ(分)
毎分80mで歩く距離： 2000－Ｌ(メートル)
毎分80mで歩く時間： 30－Ｍ(分)
次に毎分60mで歩いた時と、80mで歩いた時を別々に見ていきます。
毎分60mで歩いた時
公式にあてはめると次のようになります。
速度 ＝ 距離 ÷ 時間
60 ＝ Ｌ ÷ Ｍ ・・・(１)
毎分80mで歩いた時
公式にあてはめると次のようになります。
速度 ＝ 距離 ÷ 時間
80 ＝ (2000－Ｌ) ÷ (30－Ｍ) ・・・(２)
毎分60mで歩く距離Ｌを求める
式(１)(２)の連立方程式を解けば、求めたい毎分60mで歩く距離Ｌを求めることができます。
60 ＝ Ｌ ÷ Ｍ ・・・(１)
80 ＝ (2000－Ｌ) ÷ (30－Ｍ) ・・・(２)
式(１)を式(２)に代入することで、Ｌを求めることができます。ここは、自分のやりやすいように計算すればよいと思います。私は、まずは式(１)(２)の両方とも少し変形させてから代入させます。
式(１)を変形
60 ＝ Ｌ ÷ Ｍ ・・・(１)
Ｍ ＝ Ｌ ÷ 60
式(２)を変形
80 ＝ (2000－Ｌ) ÷ (30－Ｍ) ・・・(２)
80(30－Ｍ) ＝ (2000－Ｌ)
2400－80Ｍ ＝ 2000－Ｌ
Ｌ－80Ｍ ＝ －400
変形後の式(１)を変形後の式(２)へ代入
Ｌ－80(Ｌ/60) ＝ －400
Ｌ－4Ｌ/3 ＝ － 400
－Ｌ/3 ＝ －400
Ｌ ＝ 1200
よって、求めたい解答は1200m以内
解答：1200m以内
試験問題５の解答：
この問題は、少々難易度が高くなり、解くためにはいくつかの公式や定義を知っている必要があります。
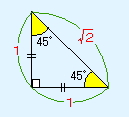知っておかなければならに1つ目は、三角比。図のように三角形が直角二等辺三角形の場合、各辺の比は、1：1：√2となります。
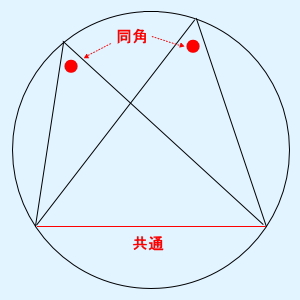次に知っておかなければならないのが、円に内接する三角形の円周角についてです。図のように2つの三角形の1辺が共通でそれに向かい合う対角が等しい場合、この2つの三角形は同じ円に内接していることが言えます。
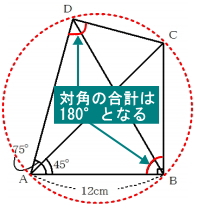最後に円に内接する四角形についても知っておく必要があります。図のように円に内接する四角形は、向かい合う対角の合計が必ず180°となります。
この3点をおさえて問題を解いていきます。
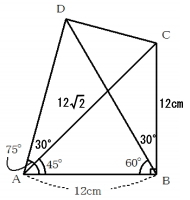
まず、三角形ＡＢＣは、直角二等辺三角形なので三角比より、
辺ＡＣ＝√2 × 12 ＝ 12√2
∠ＡＢＣ＝90°なので、∠ＤＢＣは次の通り。
∠ＤＢＣ＝90－60＝30°
∠ＤＡＢ＝75°なので、∠ＤＡＣは次の通り。
∠ＤＡＣ＝75－45＝30°
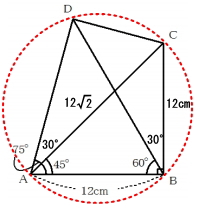したがって三角形ＤＡＣと三角形ＤＢＣは、辺ＤＣが共通、対角が30°で等しいので同じ円に内接することが言えます。つまり、四角形ＡＢＣＤは、円に内接する四角形となります。
よって、
∠ＡＤＣ=180－∠ＡＢＣ=180－90＝90°
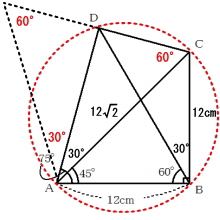∠ＤＡＣ＝30°なので、∠ＡＣＤ＝60となります。このことから、三角形ＤＡＣは、正三角形(正三角形は全ての角が60°)の半分の三角形だということが分かります。
よって、辺ＡＣの半分が辺ＣＤの長さになります。
ＤＣ＝ＡＣ÷2
＝12√2 ÷ 2
＝6√2
解答：6√2cm
