次の問に答えなさい。
[問題1] りんご1個の値段はみかん1個の値段より30円高いです。りんご8個とみかん6個を買ったとき、合計代金が 1,360円でした。このとき、りんご1個の値段は何円ですか。ただし、消費税は考えないものとします。
[問題2] 歯数が48の歯車Ａと歯数が36の歯車Ｂがかみあって回転しています。歯車Ａが9回転するとき、歯車Ｂは何回転しますか。
[問題3] 男女合わせて36人在籍するクラスでテストをしました。男子の平均点が71点、女子の平均点が80点、クラス全体の平均点は75点でした。このとき、クラスの男子の人数は何人ですか。
[問題4] 100円玉3枚と50円玉2枚を同時に投げたとき、表になった硬貨の合計金額が250円以上になる確率を分数で求めなさい。
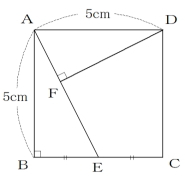
[問題5] 図のような1辺の長さが5cmの正方形ＡＢＣＤがあります。点ＡとＢＣの中点Ｅとを結んだ線分ＡＥに点Ｄから垂線を引き、その交点をＦとします。 このとき、四角形ＣＤＦＥの面積は何cm2ですか。ただし、分数で答えなさい。
解答と解説
試験問題１の解答：
求めたいりんご1個の値段をＸと仮定すると、りんごとみかん1個の値段は次のように表すことができます。
りんご1個の値段： Ｘ
みかん1個の値段： Ｘ－30
また、りんご8個とみかん6個を買ったとき、合計代金が 1,360円ということなので次の式が成り立ちます。
8Ｘ ＋ 6(Ｘ－30)＝1360
この式を解くと、求めたいりんご1個の値段Ｘが求まります。
8Ｘ ＋ 6(Ｘ－30)＝1360
14Ｘ＝1360＋180
14Ｘ＝1540
Ｘ＝110
解答：110円
試験問題２の解答：
歯数が48の歯車が9回転した場合、歯車ＡとＢの接点を通過した歯数は次の通り。
接点を通過した歯数＝48×9＝432
歯車Ｂの歯数は36なので、1回転あたり接点を36の歯が通過することになる。よって、432の歯数が通過した場合、歯車Ｂが回った回転数は次の通り。
歯車Ｂの回転数＝432÷36＝12
解答：12回転
試験問題３の解答：
求めたい男子の人数をＸと仮定した場合、男子と女子の人数は次のようになります。
男子人数： Ｘ
女子人数： 36－Ｘ
男子の平均点が71点なので、男子全員の合計得点は次の通り。
男子の合計得点＝71Ｘ
女子の平均点が80点なので、女子全員の合計得点は次の通り。
女子の合計得点＝80(36－Ｘ)＝2880－80Ｘ
男女合わせたクラス全員の平均点が75点ということなので次の式が成り立ちます。
男女合計得点 ÷ 男女人数 ＝ 男女平均得点
(71Ｘ＋2880－80Ｘ) ÷ (Ｘ＋36－Ｘ)＝75
この式を解くと求めたい男子の人数Ｘが求まります。
(71Ｘ＋2880－80Ｘ) ÷ (Ｘ＋36－Ｘ)＝75
(2880－9Ｘ) ÷ 36 ＝ 75
2880－9Ｘ ＝ 75 × 36
－9Ｘ ＝ 2700 － 2880
－9Ｘ ＝ －180
Ｘ ＝ 20
解答：20人
試験問題４の解答：
金額の合計が250円以上になる確率を求めるには、次の計算をする必要があります。
確率＝(250円以上になる組み合わせ数) ÷ (総組合せ数)
よって、まずは『250円以上になる組み合わせ数』と『総組合せ数』を算出しなければなりません。『250円以上になる組み合わせ数』を求めるには組み合わせの公式を利用します。組み合わせの公式は次の通り。
250円以上になる組み合わせ数
合計金額が250円以上になるためには、100円玉、50円玉はそれぞれ次の枚数表になる必要があります。
①100円が3枚表向きで、50円はすべての組み合せ——>3c3×(2^2)=4
②100円が2枚表向きで、50円が1枚以上表向きの組み合わせ——>3c2×(2c2+2c1)=3×(1+2)=9
(100円が2枚)かつ(50円が1枚)
(100円が2枚)かつ(50円が2枚)
(100円が3枚)かつ(50円が0枚)
(100円が3枚)かつ(50円が1枚)
(100円が3枚)かつ(50円が2枚)
そして、これらの組み合わせ数を求める必要があります。
(100円が2枚)かつ(50円が1枚)となる組み合わせ数
3Ｃ2 × 2Ｃ1
＝(3×2)/(2×1) × (2/1)
＝3 × 2
＝6
(100円が2枚)かつ(50円が2枚)となる組み合わせ数
3Ｃ2 × 2Ｃ2
＝(3×2)/(2×1) × (2×1)/(2×1)
＝3 × 1
＝3
(100円が3枚)かつ(50円が0枚)となる組み合わせ数
3Ｃ3 × 2Ｃ0
＝(3×2×1)/(3×2×1) × 1
＝1 × 1
＝1
2Ｃ0 は、0では？ となりがちなのですが、『nＣr』のn、rは本来1以上定義されており、r＝0となる場合は、『nＣr＝nＣ0＝1』となります。
(100円が3枚)かつ(50円が1枚)となる組み合わせ数
3Ｃ3 × 2Ｃ1
＝(3×2×1)/(3×2×1) × (2/1)
＝1 × 2
＝2
(100円が3枚)かつ(50円が2枚)となる組み合わせ数
3Ｃ3 × 2Ｃ1
＝(3×2×1)/(3×2×1) × (2×1)/(2×1)
＝1 × 1
＝1
これらの合計が250円以上となる組み合わせすうになります。
6＋3＋1＋2＋1＝13通り
総組合せ数
100円玉3枚を投げたときの裏表の組み合わせ数を求めます。1枚の硬貨は裏表の2パターン存在し、これが3枚あるので組み合わせ数は次の通り。
2×2×2＝8通り
次に同じように50円玉2枚を投げたときの組合数を求めます。1枚の硬貨は裏表の2パターン存在し、これが2枚あるので組み合わせ数は次の通り。
2×2＝4通り
よって、総組合せ数は次の通り。
8×4＝32通り
確率を求める
総組合せ数32通り、その内、250円以上になる組み合わせ数が13通りと分かりました。よって、求める確率は次の通り。
確率＝13÷32＝13/32
解答：13/32
試験問題５の解答：
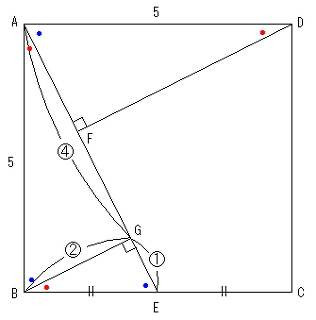頂点Ｂから線分ＡＥに垂線ＢＧを引くと、角の関係により △ＢＧＥ、△ＡＧＢ、△ＤＦＡは すべて△ＡＢＥと相似で、ＡＢ＝ＤＡより △ＡＧＢと△ＤＦＡは合同となります。
△ＡＢＥ＝5×(5/2)×1/2＝25/4 (c㎡)
ＥＧ：ＢＧ＝ＥＢ：ＡＢ＝1：2
ＢＧ：ＡＧ＝ＥＢ：ＡＢ＝1：2＝2：4
よって、ＥＧ：ＡＧ＝1：4
△ＡＧＢ＝△ＡＢＥ×ＡＧ/ＡＥ＝(25/4)×4/(1+4)＝5 (c㎡)
△ＤＦＡ＝△ＡＧＢ＝5 (c㎡)
四角形ＣＤＦＥ＝正方形ＡＢＣＤ－△ＤＦＡ－△ＡＢＥ
＝5×5－5－(25/4)
＝55/4 (c㎡)
しかし、計算はここで終わらないようにしたい。
問題用紙の初めに記載されている注意事項に次のような事項が記されています。
よって、55/4＝13(3/4) まで計算をしておきたい。
解答：13(3/4)
