次の問に答えなさい。
[問題1] 2けたの素数を大きい方から小さい方に順に並べたとき、大きい方から5番目の素数はいくつですか。
[問題2] 歯数24の歯車Aと歯数60の歯車Bがかみあって回転していて、歯車Aは5分間に15回転します。このとき,歯車Bは5分間に何回転しますか。
[問題3] 2けたの自然数があります。十の位の数と一の位の数を入れかえて出来る数は、もとの数より18大きくなりますが,もとの数の2倍よりは17小さくなります。このとき,もとの自然数を求めなさい。
[問題4] Xを自然数とするとき、√19-Xの値が整数となるようなXの値のうち一番小さい数を求めなさい。
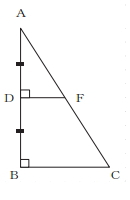
[問題5] 図のような直角三角形ABCがあります。辺ABの中点Dから辺ABに垂直な線を引き、辺ACとの交点をFとします。三角形ADFの面積をS1,四角形DBCFの面積をS2としたとき、S1:S2 を最も簡単な整数の比で表しなさい。
解答と解説
試験問題1の解答:
1と自分自身以外に正の約数を持たない自然数で、1でない数のこと。 と、Wikipediaにはありますが、約数などを知らない人にとっては何のこっちゃ? と思うでしょう。
素数とは、『1より大きい整数で、1とその数以外で割り切れない数』のことです。 例えば、『5』は1より大きい整数で、1と5でしか割り切れないので素数になります。2で割ったら2.5で割り切れるのでは? とひねくれないように。あくまで、整数で割り切れる数が対象です。
次に、数字の『6』は1と6以外にも2や3でも割り切れるので、素数ではありません。
いくつか、素数の例をあげると次のような数字です。全て、1とその数字でしか割り切れないはずです。
2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59 ~
この問題は、力技で解くのが一番いい。2桁の素数なので99から順番に下の数字を見ていき、1とその数以外で割り切れるかどうかを確認する。
99 3,9,11,33で割り切れる
98 2,7,14,49で割り切れる
97 素数
96 2,3,4,6,8,12,16,24,32,48で割り切れる
95 5,19で割り切れる
94 2,47で割り切れる
93 3,31で割り切れる
92 2,4,23,46で割り切れる
91 7,13で割り切れる
90 2,3,5,6,9,10,15,18,30,45で割り切れる
89 素数
88 2,4,8,11,22,44で割り切れる
87 3,29で割り切れる
86 2,43で割り切れる
85 5,17で割り切れる
84 2,3,4,7,12,21,28,42で割り切れる
83 素数
82 2,41で割り切れる
81 3,9,27で割り切れる
80 2,4,5,8,10,16,20,40で割り切れる
79 素数
78 2,3,6,13,26,39で割り切れる
77 7,11で割り切れる
76 2,4,19,38で割り切れる
75 3,5,15,25で割り切れる
74 2,37で割り切れる
73 素数
よって、2桁の素数で大きい方から5番目の素数は、73
これを本番で全部順番で計算していくの? 大変では? と思う方もいるかもしれませんが、コツを知っていれば意外に簡単に計算ができます。素数ではない割り切れる数を見てください。
全て、『2』『3』『5』『7』のいずれかの数値で割り切れるのです。また、『2』で割り切れる数が最も多く、次いで『3』『5』『7』となります。
よって、今回の様に素数を探す場合はまずは、『2』で割り切れるかを確認します。割り切れたら素数ではないとその時点で分かるので、それ以降は確認する必要はありません。もし、『2』で割り切れない場合は『3』ではどうか? と順に確認し、『7』まで割り切れなければそれは素数になります。
解答:73
試験問題2の解答:
歯数24の歯車Aについて
歯数が24枚なので、歯車Bとの接点を1回転で24枚の歯が通過することになる。よって、15回転した場合は、360枚(24×15枚)の歯が通過したことになる。
歯数60の歯車Bについて
歯車Bの歯数は60枚なので、歯車Bが1回転で歯車Aとの接点を通過する枚数は、60枚。
よって、360枚の歯を通過させるには、6回転(360÷60)しなければならないことになる。
解答:6回転
試験問題3の解答:
自然数とは、1以上の整数のことで、簡単な覚え方としては、自然界にあり得る数字と覚えればいい。0は、無なので自然界にはない数字。昆虫の数が0というのは自然界にいないことになりますよね。1.5や3.2などの小数も自然界には無い数字。昆虫が1.5匹います! って体半分? となりますよね。
自然数は、1、2、3、4、5、6、~
という1以上の整数を表します。
2桁の自然数なので10~99のいずれかの整数ですよね。求める自然数の十の位の値をMと仮定し、一の位の値をNと仮定して計算します。
元の自然数は次の式で表すことができます。
元の自然数=(M×10)+N ・・・(1)
十の位の数と一の位の数を入れかえて出来る数は次の式で表すことができます。
入れ替え後の自然数=(N×10)+M ・・・(2)
十の位の数と一の位の数を入れかえて出来る数は,もとの数より18大きくなということなので式(2)-式(1)は18となるはず。よって、次の式で表すことができます。
式(2)-式(1)=18
(N×10)+M-{(M×10)+N}=18
10N+M-10M-N=18
9N-9M=18
N-M=2 ・・・(3)
次に、もとの数の2倍よりは17小さいということなので次の式が成り立ちます。
元の自然数 × 2 - 17 = 入れ替え後の自然数
{(M×10)+N} × 2 - 17 = (N×10)+M
20M+2N-17=10N+M
19M-8N=17 ・・・(4)
式(3)と式(4)の連立方程式を解けば、求めたい元の数値が出てきます。
N-M=2 ・・・(3)
19M-8N=17 ・・・(4)
式(3)を式(4)へ代入します。
19M-8(2+M)=17
19M-16-8M=17
11M=33
M=3
M=3を式(3)へ代入
N-M=2
N-3=2
N=5
よって、元の自然数は、35
解答:35
試験問題4の解答:
√19-Xが整数になるためには、求める整数をMとした場合、ルート内が√M²のように2乗にならなければならない。要は、次のような式が成り立たなければならないということです。
19-X=M²
Xは自然数なので1~18しかない。その内、最も小さい数値を求めるので1から順にあてはめる力技でよい。
X=1の場合
19-1=M²
18=M²
M×Mが18になる整数は無いのでX=1は違う。
X=2の場合
19-2=M²
17=M²
M×Mが17になる整数は無いのでX=2も違う。
X=3の場合
19-3=M²
16=M²
M×Mが16になる整数は4がある。よって、X=3が最も小さい数。
解答:3
試験問題5の解答:
まず、最初に気が付かなければならないのが、三角形ADFと三角形ABCは相似だとうことです。
2つの三角形が相似になる条件は次の3つがあり、いずれか1つでもあてはまればその2つの三角形は相似だと言えます。
(1)3組の辺の比が、すべて等しいとき
(2)2組の辺の比とその間の角が、それぞれ等しいとき
(3)2組の角が、それぞれ等しいとき
今回の設問であれば、(3)が該当します。∠Aは共通なので等しい、∠D=∠B=90°なので等しい。当然残る1つの角も等しいことになります。
また、2つの三角形が相似の場合、次のことが言えます。
・対応する線分の長さの比は、すべて等しい。
・対応する角の大きさは、それぞれ等しい。
三角形ADFの面積を求める
三角形ADFの面積S1は、底辺をDF、高さはADのとした場合、次の式で表すことができます。
S1 = DF × AD ÷ 2
三角形ABCの面積を求める
ADは、ABの中点なので三角形ABCの高さABはAD×2で表すことができます。また、ポイントに記載した通り、三角形ADFと三角形ABCは相似です。辺AD:ABが1:2の相似なので、他の辺も全て1:2になります。(相似の場合、対応する線分の長さの比は、すべて等しい。←ポイント参照)
よって、底辺をBCは、DF×2で表すことができます。三角形ABCの面積をS3とした場合、次の式で表すことができます。
S3 = (DF×2) × (AD×2) ÷ 2
四角形DBCFの面積を求める
四角形DBCFの面積は、三角形ABCの面積から三角形ADFの面積を引くことで求められます。よって、四角形DBCFの面積S2は次の通り。
S2 ={(DF×2) × (AD×2) ÷ 2} - {DF × AD ÷ 2}
=2(DF)(AD)-(DF)(AD)/2
=(3/2)(DF)(AD)
よって、下記のようにS1とS2が分かりました。
S1 = DF × AD ÷ 2
=(1/2)(DF)(AD)
S2 =(3/2)(DF)(AD)
S1 : S2 = (1/2)(DF)(AD) : (3/2)(DF)(AD)
となります。このままだと分かり難いので、右辺の共通分部である(1/2)(DF)(AD) を取り除くと次のようになります。
S1 : S2 = 1 : 3
解答:S1 : S2 = 1 : 3

