東京 職業訓練 試験問題[筆記試験] 数学-問2(1)(2)【平成28年7月生】

試験問題 問２(１)

１周7.2㎞の池があります。池の周囲のある地点からＡ君は分速60ｍで歩き始め、同時刻に同じ地点からＢ君はＡ君と反対向きに分速180ｍで走り始めるとき、２人が出会うのは何分後ですか。

解答と解説

問２(１)の解答：30分後

この問題を解くには速度と距離と時間を求める公式を知っている必要があります。

問題文から分かっている点を図に書き込むと下図のようになります。

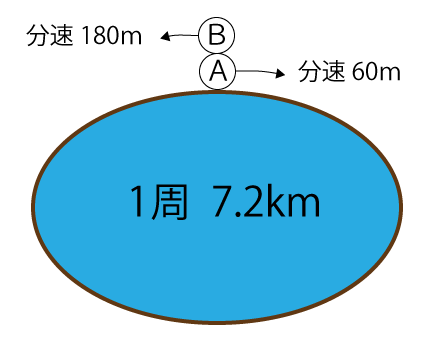
Ａ君の移動距離とＢ君の移動距離を求め、二人の移動距離の合計が池の1周の距離に等しくなった時が出会う時になります。よって、次の流れで求めていきます。

Ａ君の移動距離を求める

スタートしてから二人が出会うまでの時間をＨ分と仮定すると、その時の移動距離は下記のようにあらわすことができます。

距離＝速度×時間
　　＝60Ｈ・・・①

Ｂ君の移動距離を求める

スタートしてから二人が出会うまでの時間をＨ分と仮定すると、その時の移動距離は下記のようにあらわすことができます。

距離＝速度×時間
　　＝180Ｈ・・・②

二人が出会う時間を求める

Ａ君の移動距離①とＢ君の移動距離②を合計すると池の1周の距離7.2kmに等しくなるはずなので以下の式が成り立ちます。

①＋②＝7200

ここで、距離の単位をｍに統一することを忘れないようにしてください。移動速度はｍ/分であらわされているので、距離はｍ、時間は分で統一する必要があります。

60Ｈ＋180Ｈ＝7200
240Ｈ＝7200
24Ｈ＝720
Ｈ＝30

よって、二人が初めて出会うのは30分後

試験問題 問２(２)

赤玉が２個と白玉が４個入っている袋があります。この袋から同時に２個の玉を取り出すとき、少なくとも１つが赤玉となる確率を分数で求めなさい。

解答と解説

問２(２)の解答：3/5

少なくとも１つが赤玉となる確率は、以下の式で求めることができます。

また、組み合わせ数を求める公式は次の通りです。

よって、次の流れで求めていきます。

袋の中から2個の玉を取り出す組み合わせ数

袋の中には赤玉が2個、白玉が4個の計6個の玉が入っています。この中から2個の玉を取り出す組み合わせ数は、組み合わせ数を求める公式より次の通りになります。

₆Ｃ₂＝(6×5×4×3×2×1)/{(2×1)(4×3×2×1)}
　　＝(6×5)/(2×1)
　　＝15通り

取り出した玉に赤玉が含まれている組み合わせ数

これは素直に赤玉が含まれている組み合わせ数を考えるのではなく、その反対の取り出した2個の玉が『すべて白玉である組み合わせ数』を考えるようにした方が簡単です。

取り出した2個の玉がすべて白玉である場合、白玉4個の中から2個が選ばれる必要があります。よって、その組み合わせ数は次の通り。

₄Ｃ₂＝(4×3×2×1)/{(2×1)(2×1)}
　　＝(4×3)/(2×1)
　　＝6通り

袋の中から2個の玉を取り出す場合の組み合わせ数は全15通り。その内、取り出した2個の玉が両方白玉になる組み合わせ数は6通り。

よって、取り出した2個の玉が少なくとも1つが赤玉になる組み合わせ数は15－6＝9通り。

少なくとも1つが赤玉となる確率

袋の中から2個の玉を取り出す場合の組み合わせ数は全15通り。取り出した2個の玉が少なくとも1つが赤玉になる組み合わせ数は9通り。よって、少なくとも1つが赤玉となる確率は次の通り。

少なくとも1つが赤玉となる確率＝9/15
　　　　　　　　　　　　　　＝3/5

※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。