この問題は平成28年7月入校の東京都立職業能力開発センター入校選考試験問題の問2の(3)と(4)の解答と解説です。
問1および、問2の(1)(2)(5)に関しては以下のページに解説をまとめているので参考にして下さい。
実際の試験の問題用紙は以下のページで確認することができます。
■目次
試験問題 問2(3)
2けたの自然数があります。その数の2倍は、十の位の数と一の位の数の和の8倍に等しく、また十の位の数と一の位の数を入れかえてできる2けたの自然数は、もとの数より18大きくなります。もとの自然数はいくつですか。
解答と解説
問2(3)の解答:24
自然数とは簡単に言うと自然界のものを数えるときに使う数字「1,2,3,4・・・」です。木や動物を数えるときにマイナスや小数は使わないですよね。
元の自然数の十の位の数字をa、一の位の数字をbと仮定すると元の数字は下記のようにあらわすことができます。
元の自然数=a×10+b
=10a+b
元の数の2倍は、十の位の数と一の位の数の和の8倍に等しということなので以下の式が成り立ちます。
(10a+b)×2=(a+b)×8
20a+2b=8a+8b
12a-6b=0・・・①
さらに十の位の数と一の位の数を入れかえてできる2けたの自然数は、もとの数より18大きくなるということなので以下の式が成り立ちます。
(10b+a)=(10a+b)+18
9a-9b+18=0
a-b+2=0
a=b-2・・・②
式②のaを式①のaへ代入します。
12a-6b=0・・・①
12(b-2)-6b=0
12b-24-6b=0
6b=24
b=4
b=4を式②へ代入してaの値も求めます。
a=b-2・・・②
a=4-2
=2
よって、元の自然数は24
試験問題 問2(4)
底面が1辺5cmの正方形で、側面は高さが4cmの二等辺三角形である正四角すいがあります。この正四角すいの表面積は何㎝²ですか。
解答と解説
問2(4)の解答:65cm²
問題文から分かっている点を図に書き込むと下図のような正四角すいになります。
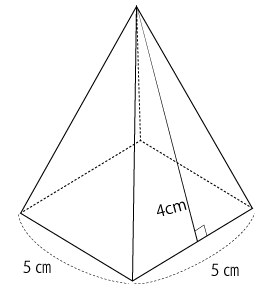
表面積は底面の正方形と、側面の二等辺三角形に分けて計算し、最後に合計します。
解くまでの流れ
- 底面の正方形の面積を求める
- 側面の二等辺三角形の面積を求める
- 正四角すいの表面積を求める
底面の正方形の面積を求める
正方形の一辺の長さは5㎝なので面積は次の通り。
正方形の面積=5×5
=25cm²・・・①
側面の二等辺三角形の面積を求める
側面の三角形の底辺の長さは5cm、高さは4cmなので面積は次の通り。
二等辺三角形の面積=5×4÷2
=10cm²
この二等辺三角形が4つあるので、側面の面積の合計は次の通り。
側面積=10×4
=40cm²・・・②
正四角すいの表面積を求める
正四角すいの表面積は、『底面積①+側面積②』なので次の通りになります。
正四角すいの表面積=25+40
=65cm²
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

