この問題は平成28年7月入校の東京都立職業能力開発センター入校選考試験問題の問2の(5)の解答と解説です。
問1および、問2の(1)~(4)に関しては以下のページに解説をまとめているので参考にして下さい。
実際の試験の問題用紙は以下のページで確認することができます。
試験問題 問2(5)
図の円で、弦AB、弦CDを延長し、交わった点をPとするとき、BPの長さは何cmですか。
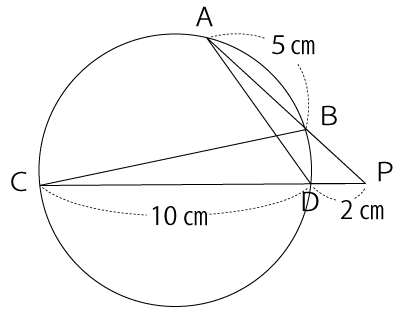
解答と解説
問2(5)の解答:3cm
この問題を解くには『三角形の相似条件』と『円の性質』の2点を知っている必要があります。
三角形の相似条件
- 3組の辺の比がすべて等しい
- 2組の辺の比とその間の角が等しい
- 2組の角が等しい
円の性質は色々ありますが、今回知っておく必要があるのは『同じ弧を持つ円周角は等しい』という点です。
下図のように弧BDが共通の場合、∠BADと∠BCDは等しい角度になります。
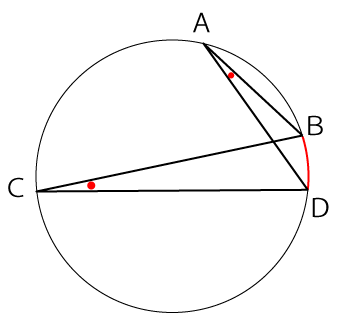
問題にもどって再度、今回の問の図を確認してみてください。

△PDAと△PBCは、∠PAD=∠PCBで∠Pが共通なので『2組の角が等しい』の相似条件を満たしているので相似な三角形になります。
よって、以下の式が成り立ちます。
PA:PC=PD:PB
求めたいBPの長さをNcmと仮定した場合、上記の式は次のようになります。
PA:PC=DP:BP
(5+N):12=2:N
上記の式を解けば求めたいBPの長さNが求まります。
(5+N):12=2:N
(5+N)×N=2×12
N²+5N-24=0
(N-3)(N+8)=0
N=3、-8
長さにマイナスはないので、BPの長さは3cm
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

