この問題は平成29年1月入校の東京都立職業能力開発センター入校選考試験問題の問2の(5)の解答と解説です。
問1および、問2の(1)~(4)に関しては以下のページに解説をまとめているので参考にして下さい。
実際の試験の問題用紙は以下のページで確認することができます。
試験問題 問2(5)
図は、正三角形ABCを、頂点Aが辺BC上の点Fに重なるように、線分DEを折り目として折ったものです。BF=6cm、FD=14cm、DB=16cmのとき、もとの正三角形の線分AEの長さは何cmですか。
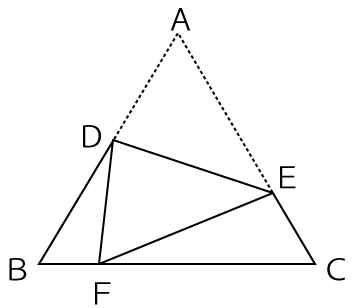
解答と解説
問2(5)の解答:21cm
この問題を解くには三角形の相似条件を知っている必要があります。
三角形の相似条件
- 3組の辺の比がすべて等しい
- 2組の辺の比とその間の角が等しい
- 2組の角が等しい
まず最初に気が付いて欲しい点としては、△BDFと△CFEが相似な三角形であるという点です。分かる方は『線分AEの長さを求める』の章まで読み飛ばして頂いて構いませんが、相似な三角形について少し解説しておきます。
△BDFと△CFEが相似な三角形である証明
△ABCは正三角形なので、∠B=∠C=∠DFE=60°だと分かっています。
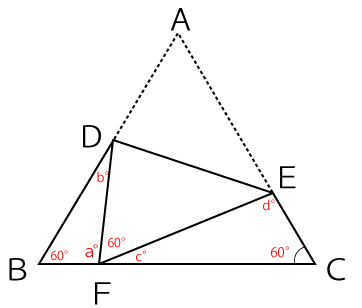
このことより以下の3つの式が成り立ちます。
a+c=120°・・・①
a+b=120°・・・②
c+d=120°・・・③
式①-③をします。
(a+c)-(c+d)=120-120
a-d=0
a=d
よって、△BDFと△CFEは相似条件の『2組の角が等しい』を満たしており、相似な三角形だと言えます。
線分AEの長さを求める
AD=DF=14cmなので、辺ABの長さは30cmだとわかります。よって、FC=30-6=24cmとなります。
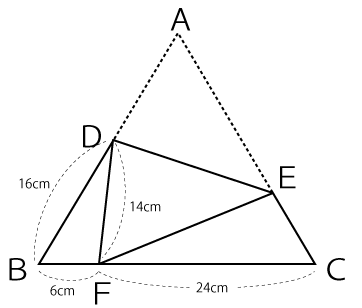
△BDFと△CFEは相似な三角形でその比は次の通り。
DB:FC=16:24
=2:3
△BDFと△CFEの各辺の長さの比は2:3になることが分かりました。よって、EFの長さは次の通り。
FD:EF=14:X
2:3=14:X
2X=42
X=21
よって、EFの長さは21cm。AE=EFなので、求めたい線分AEの長さは21cm
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

