この問題は平成29年10月入校の東京都立職業能力開発センター入校選考試験問題の問2の(1)と(2)の解答と解説です。
問1および、問2の(3)~(5)に関しては以下のページに解説をまとめているので参考にして下さい。
実際の試験の問題用紙は以下のページで確認することができます。
■目次
試験問題 問2(1)
12%の食塩水と8%の食塩水を混ぜて、食塩水を280gつくりました。できた食塩水の濃度が9%であるとき、混ぜた12%の食塩水は何gですか。
解答と解説
問2(1)の解答:70g
この問題を解くには食塩水の濃度を求める公式を知っている必要があります。

12%の食塩水が入った容器をA、8%の食塩水が入った容器をB、混ぜ合わせてできた食塩水が入った容器をCとします。また、求めたい混ぜた12%の食塩水の量をXgと仮定し、容器Cの食塩の量をMと仮定した場合、下図のようになります。
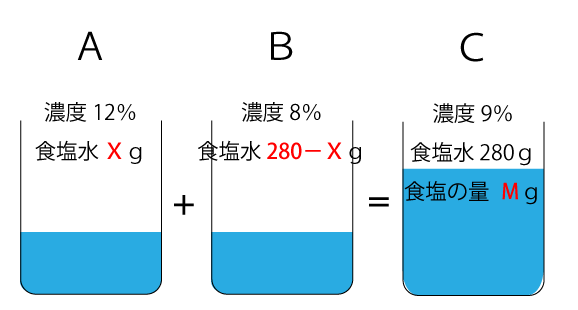
容器Cの食塩の量Mを求める
食塩水の濃度を求める公式から容器Cに入っている食塩の量は以下の通りになります。
濃度(%)={(食塩の量)/(食塩水の量)}×100
9=(M/280)×100
100M=2520
M=25.2g・・・①
容器Aの食塩の量を求める
濃度(%)={(食塩の量)/(食塩水の量)}×100
12={(食塩の量)/X}×100
食塩の量=12X/100
=3X/25・・・②
容器Bの食塩の量を求める
濃度(%)={(食塩の量)/(食塩水の量)}×100
8={(食塩の量)/(280-X)}×100
食塩の量=8(280-X)/100
=2(280-X)/25・・・③
容器Aの食塩水の量Xを求める
容器Cの食塩の量①=容器Aの食塩の量②+容器Bの食塩の量③
25.2=3X/25+2(280-X)/25
25.2=(X+560)/25
X+560=630
X=70
よって、求めたい混ぜた12%の食塩水の量は、70g
試験問題 問2(2)
よしこさんは、A地点から峠をこえて、15km離れたB地点へ行くのに、3時間30分かかりました。A地点から峠までは時速4km、峠からB地点までは時速6kmの速さで走りました。このときA地点から峠までの道のりは何kmですか。
解答と解説
問2(2)の解答:12km
この問題を解くには速度と距離と時間を求める公式を知っている必要があります。

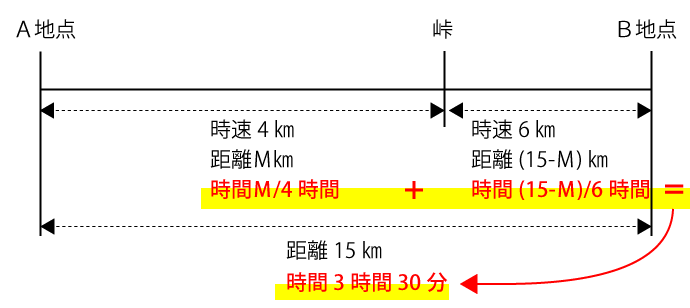
まず、分かっている点を図式化すると下図のようになります。
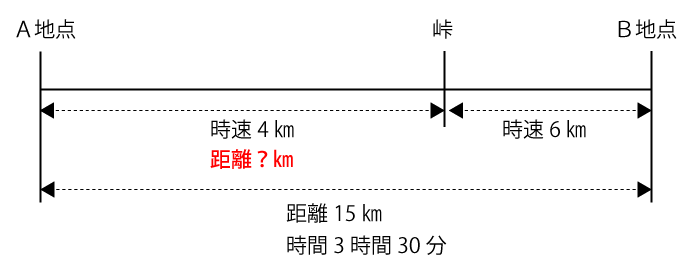
解くまでの流れ
- A地点から峠までの時間を求める
- 峠からB地点までの時間を求める
- A地点から峠までの距離を求める
では、実際に順に解いていきます。
A地点から峠までの時間を求める
最終的に求めたいA地点から峠までの距離をMkmと仮定します。
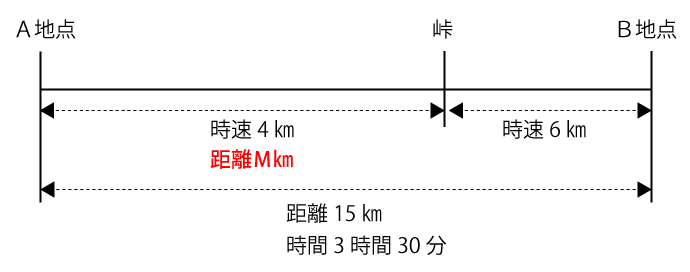
距離と時間と速度の公式より、A地点から峠までの時間は次のようにあらわすことができます。
A地点から峠までの時間=距離÷速度
=M÷4
=M/4・・・①
峠からB地点までの時間を求める
最終的に求めたいA地点から峠までの距離をMkmと仮定した場合、峠からB地点までの距離は(15-M)kmとなります。
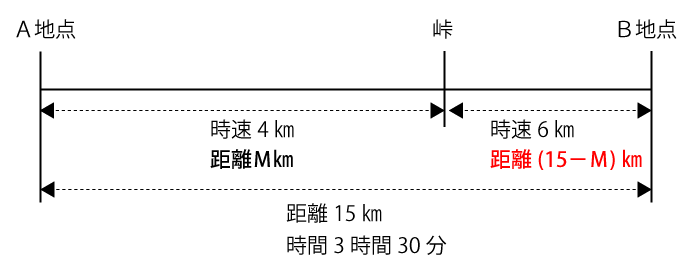
よって、距離と時間と速度の公式より、峠からB地点までの時間は次のようにあらわすことができます。
峠からB地点までの時間=距離÷速度
=(15-M)÷6
=(15-M)/6・・・②
A地点から峠までの距離を求める
A地点から峠までにかかった時間①がM/4、峠からB地点までにかかった時間②が(15-M)/6、そしてA地点からB地点までにかかった時間は問題文より3時間30分と分かっているので以下の式が成り立ちます。
(M/4)+(15-M)/6=3.5
このとき時間の単位を統一するように注意してください。30分は0.5時間です。この式を解くと求めたいA地点から峠までの距離Mが求まります。
(M/4)+(15-M)/6=3.5
左辺と右辺にそれぞれ12をかけて分数を無くし計算しやすくします。
(M/4)×12+{(15-M)/6}×12=3.5×12
3M+2(15-M)=42
M+30=42
M=12
よって、A地点から峠までの距離は12km
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

