この問題は平成29年10月入校の東京都立職業能力開発センター入校選考試験問題の問2の(5)の解答と解説です。
問1および、問2の(1)~(4)に関しては以下のページに解説をまとめているので参考にして下さい。
実際の試験の問題用紙は以下のページで確認することができます。
試験問題 問2(5)
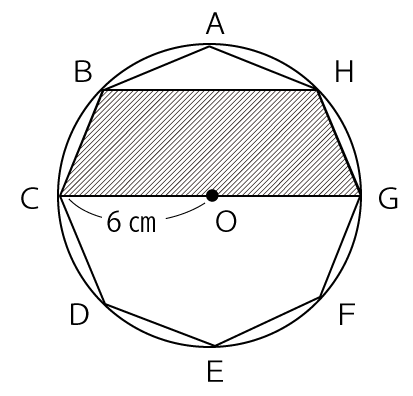
図のような半径6cmの円Oがあります。円Oの円周上に点A、B、C、D、E、F、G、Hをとり、正八角形をつくります。このとき、四角形BCGHの面積は何㎝²になりますか。
解答と解説
問2(5)の解答:18+18√2㎝²
この問題は三平方の定理やsin45°、cos45°の値を知っていれば解くことができます。今回は三平方の定理を利用して解いていきます。
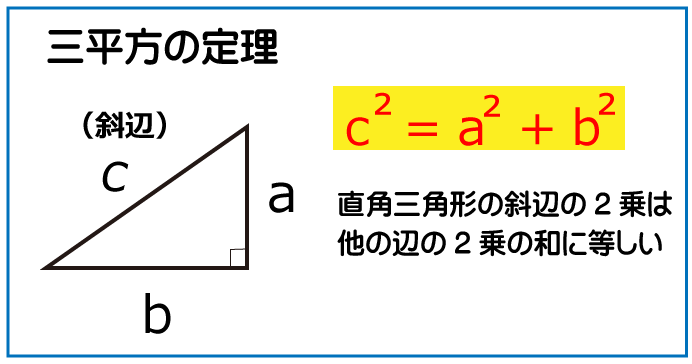
円に内接する八角形は正八角形なので、∠BOH=90°となります。また、BO、HOは円の半径なので6㎝だとわかります。
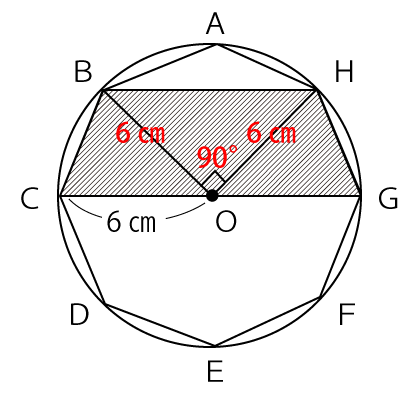
三平方の定理を利用してBHの長さを求めます。
BH²=BO²+HO²
=6²+6²
=36+36
=72
BH=√72
=6√2
次にOAとBHの交点を点Jとし、OJの長さを求めます。これが台形BCGHの高さになります。
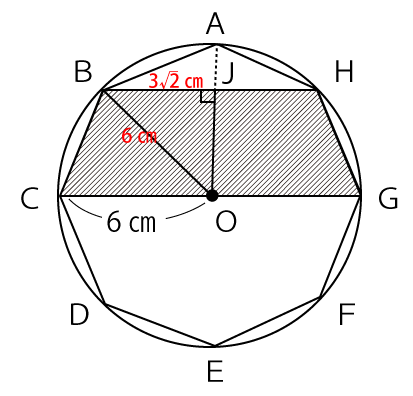
BJの長さはBHの半分の長さになるため3√2と分かります。また、∠BOJ=45°なので∠OBJも45°となり△BOJは直角二等辺三角形となります。よって、OJ=BJ=3√2となります。
台形の面積を求める公式=(上底+下底)×高さ÷2
上底=BH=6√2
下底=CG=12
高さ=OJ=3√2
よって、台形BCGHの面積は次の通り。
台形BCGHの面積=(6√2+12)×3√2÷2
=(3√2+6)×3√2
=18+18√2㎝²
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

