この問題は平成29年10月入校の東京都立職業能力開発センター入校選考試験問題の問2の(3)と(4)の解答と解説です。
問1および、問2の(1)(2)(5)に関しては以下のページに解説をまとめているので参考にして下さい。
実際の試験の問題用紙は以下のページで確認することができます。
■目次
試験問題 問2(3)
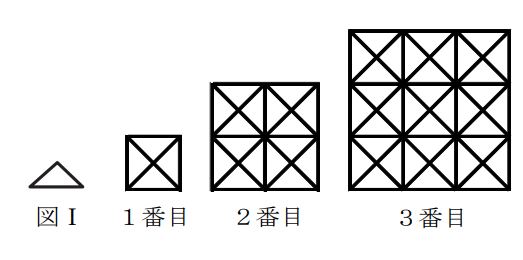
図Ⅰのような直角二等辺三角形を用いて1番目、2番目、3番目と規則的にしきつめた図形を作っていきます。図Ⅰの直角二等辺三角形を676個使ってできる図形は何番目になりますか。
解答と解説
問2(3)の解答:13番目
直角二等辺三角形4つを組み合わせてできる四角形は、1番目は1個、2番目は横に2個縦に2個の計4個、3番目は横に3個縦に3個の計9個あります。
このように横と縦の四角形の数はn番目はn個となります。よって、n番目の四角形の合計数は次の式で表すことができます。
n番目の四角形の合計数=n×n
=n²
1個の四角形で4つの直角二等辺三角形が使われているので、n番目の直角二等辺三角形の合計数は次の通りになります。
n番目の直角二等辺三角形の合計数=n²×4
このn番目の直角二等辺三角形の合計数が676個になるときのnを求めればいいので、次の式が成り立ちます。
n²×4=676
n²=676÷4
=169
n=√169
=13
よって、直角二等辺三角形を676個使ってできる図形は13番目
試験問題 問2(4)
赤い玉が3個、青い玉が4個入った袋があります。この袋の中から玉を同時に2個取り出すとき、2つとも青い玉である確率を分数で求めなさい。
解答と解説
問2(4)の解答:2/7
この問題を解くには組み合わせ数を求める公式を知っている必要があります。

袋の中の玉7個から2個を取り出す組み合わせ数は次の通り。
₇C₂=(7×6×5×4×3×2×1)/{(2×1)(5×4×3×2×1)}
=(7×6)/(2×1)
=21通り
取り出した2個が両方とも青い玉になる組み合わせ数は、4個から2個を取り出すので次の通り。
₄C₂=(4×3×2×1)/{(2×1)(2×1)}
=(4×3)/(2×1)
=6通り
よって、袋の中の玉7個から2個を取り出す組み合わせ総数が21通りある中で、2個とも青い玉が取り出される組み合わせ数は6通りあります。よって、その確率は次の通り。
2つとも青い玉である確率=6/21
=2/7
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

