この問題は平成30年10月入校の東京都立職業能力開発センター入校選考試験問題の問2の(1)と(2)の解答と解説です。
問1および、問2の(3)~(5)に関しては以下のページに解説をまとめているので参考にして下さい。
実際の試験の問題用紙は以下のページで確認することができます。
■目次
試験問題 問2(1)
歯数12の歯車Aと歯数36の歯車Bがかみ合って回転しています。歯車Aが3分間に12回転の速さで回転するとき、歯車Bが24回転するのにかかる時間は何分ですか。
解答と解説
問2(1)の解答:18分
歯車Bの歯数は歯車Aの歯数の3倍(36÷12)あるので、歯車Aが3回転して始めて歯車Bが1回転することが分かります。
歯車Aが3回転=歯車Bが1回転
また、上記のことから歯車Bが24回転するには歯車Aが72回転(24×3)しなければならないことになります。
歯車Aが72回転=歯車Bが24回転
よって、歯車Aが72回転する時間を求めれば、その時間は歯車Bが24回転する時間に等しいことになります。歯車Aは3分間に12回転するので、72回転するのにかかる時間は次の通り。
歯車Aが72回転するのにかかる時間=72÷12×3
=18
よって、歯車Bが24回転するのにかかる時間は18分
試験問題 問2(2)
5%の食塩水120gに水を加えて濃度を3%にするとき、加える水は何gですか。
解答と解説
問2(2)の解答:80g
この問題を解くには、食塩水の濃度を求める公式を知っている必要があります。
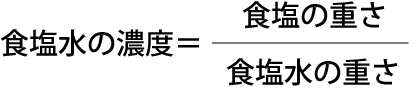
濃度は%で表すことが一般的で、通常公式には%変換するために100がかけられていますが、上記の式にはあえてかけていません。その方が覚えやすいですよね?ただ、解答を%で表すさいは100をかけることを忘れないようにしてください。
問題文より分かっている点を図式化すると下図のようになります。
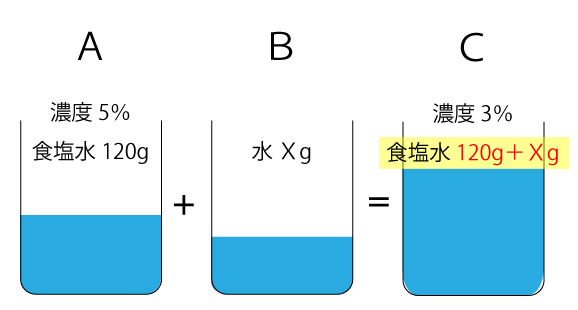
まずは、容器Aの食塩の量を求めます。
食塩水の濃度=食塩の重さ(量)÷食塩水の重さ(量)
5%=食塩の重さ(量)÷120g
食塩の重さ(量)=0.05×120
=6g
容器Bは単なる水なので、容器Cの食塩の量も6gということになります。
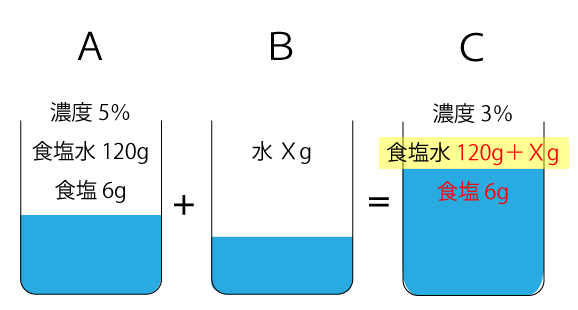
容器Cの食塩の量が分かりました。容器Bの水の量をXgと仮定した場合、公式より以下の式が成り立ちます。
食塩水の濃度=食塩の重さ(量)÷食塩水の重さ(量)
3%=6g÷(120g+Xg)
0.03=6÷(120+X)
(120+X)=6÷0.03
120+X=200
X=80
よって、加えるミズノ量は80g
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

