この問題は平成30年10月入校の東京都立職業能力開発センター入校選考試験問題の問2の(3)と(4)の解答と解説です。
問1および、問2の(1)(2)(5)に関しては以下のページに解説をまとめているので参考にして下さい。
実際の試験の問題用紙は以下のページで確認することができます。
■目次
試験問題 問2(3)
2点(3,2)、(9,-2)を通る直線とx軸、y軸で囲まれた三角形を、x軸の周りに1回転してできる円すいの体積は何㎝³ですか。ただし、1目盛を1cmとします。
解答と解説
問2(3)の解答:32π ㎝³
この問題を解くには2点を通る直線の式および、円すいの体積を求めることができる必要があります。
問題を解くのに必要な知識
- 2点を通る直線の式を求められる
- 円すいの体積を求められる
問題文を図式化すると下図のようになり、直線とx軸、y軸で囲まれた三角形は黄色で囲まれた部分になります。
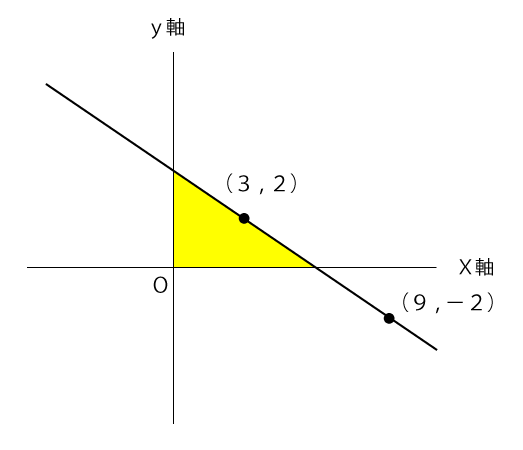
この黄色の領域がX軸の周りに1回転してできる円すいは下図の通りです。
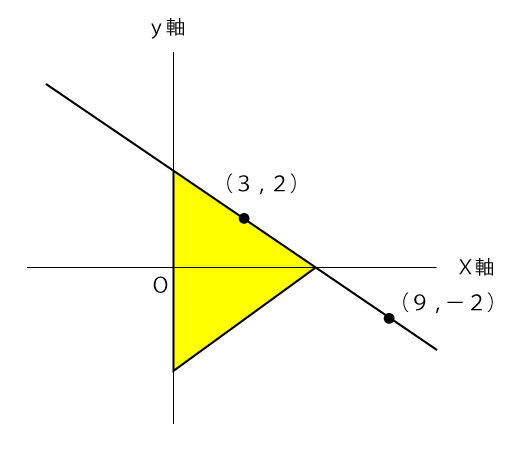
円すいの体積を求める公式は次の通り。
円すいの体積=底面積×高さ÷3
直線とy軸との交点をA、X軸との交点をBとした場合、OAの長さが円すいの底面の円の半径、OBが円すいの高さとなります。よって、点Aのy座標と点BのX座標を求めれば円すいの体積が求まります。
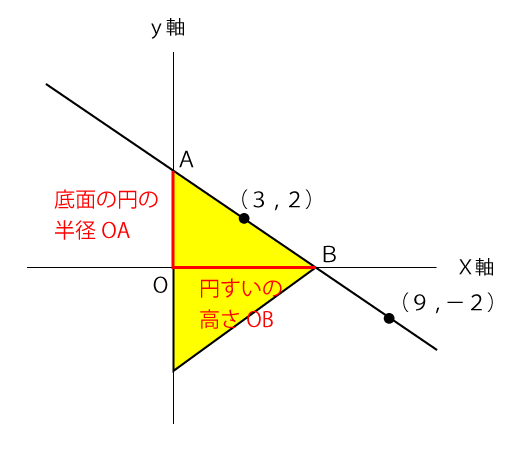
直線とX軸、Y軸の交点ABの座標を求めるにはまずは、直線の式を求める必要があります。
一次関数の直線の式は傾きをa、切片をbとした場合、次の式で表すことができます。
y=aX+b
この直線は、2点(3,2)、(9,-2)を通るので上記式にXとyの値を代入すると次のようになります。
(3,2)を代入
y=aX+b
2=3a+b・・・①
(9,-2)を代入
y=aX+b
-2==9a+b・・・②
式①-式②をしてaとbの値を求めていきます。
2=3a+b・・・①
-2==9a+b・・・②
—————–
2-(-2)=(3a+b)-(9a+b)
4=-6a
a=-2/3
aの値が求まったので式①もしくは式②にaの値を代入し、bの値も求めます。
2=3a+b・・・①
2=3×(-2/3)+b
2=-2+b
b=4
よって、直線の式は次の通り。
y=-2/3X+4
切片である4がy軸との交点のy座標になるので点A(0,4)となります。点Bはy=0なので上記直線式に代入するとX座標も求まります。
y=-2/3X+4
0=-2/3X+4
2/3X=4
X=6
よって、点B(6,0)となります。
これにより、円すいの底面である円の半径が4cm、円すいの高さが6cmと分かりました。よって、円すいの体積は次の通り。
円すいの体積=底面積×高さ÷3
=4×4×π×6÷3
=32π
よって、円すいの体積は32π ㎝³
試験問題 問2(4)
2けたの自然数があります。この数の一の位の数字から十の位の数字を引くと2になり、 十の位の数字と一の位の数字を入れかえてできる数と、もとの数の比が7:4になるとき、もとの数を求めなさい。
解答と解説
問2(4)の解答:24
元の数字の十の位の自然数をa、一の位の自然数をbと仮定します。
問題文より一の位の数字から十の位の数字を引くと2になるということなので以下の式が成り立ちます。
b-a=2・・・①
また、元の数字は以下のようにあらわすことができます。
元の数字=a×10+b・・・②
さらに十の位の数字と一の位の数字を入れかえてできる数は以下のようにあらわすことができます。
入れ替えた数字=b×10+a・・・③
入れ替えた数字と元の数字の比が7:4なので以下の式が成り立ちます。
入れ替えた数字③:元の数字②=7:4
b×10+a:a×10+b=7:4
ここで以下の比の計算方法を知っている必要があります。

b×10+a:a×10+b=7:4
(b×10+a)×4=(a×10+b)×7
40b+4a=70a+7b
66a-33b=0
2a-b=0
b=2a
b=2aだと分かりました。これを式①へ代入し、aとbの値を求めます。
b-a=2・・・①
2a-a=2
a=2
b=2aなのでbの値は次の通り。
b=2a
=2×2
=4
よって、元の数字は24
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

