この問題は平成30年10月入校の東京都立職業能力開発センター入校選考試験問題の問2の(5)の解答と解説です。
問1および、問2の(1)~(4)に関しては以下のページに解説をまとめているので参考にして下さい。
実際の試験の問題用紙は以下のページで確認することができます。
試験問題 問2(5)
図のように、1辺が18cmの正方形ABCDの紙を線分EHを折り目として折り返したところ、点Aが辺BC上にきました。辺BC上にきた点をFとします。このとき、BF:FC=1:2であるならば、四角形EFGHの面積は何cm²ですか。
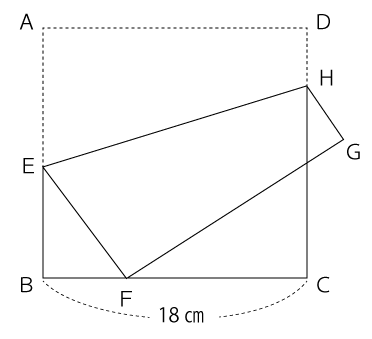
解答と解説
問2(5)の解答:126㎝²
問題文より、BF:FC=1:2と分かっているので、BFとFCの長さは次の通り。
BF:FC=1:2
FC=2BF・・・①
BF+FC=18
FC=18-BF・・・②
式②を式①へ代入し、BFとFCの長さを求めていきます。
18-BF=2BF
3BF=18
BF=6
よって、FC=12
BFとFCの比が1:2なのでBC(18㎝)を3等分してその内の2にあたる6㎝×2=12㎝がFC、1にあたる6㎝がBFと頭の中で計算できるようにしたいところです。
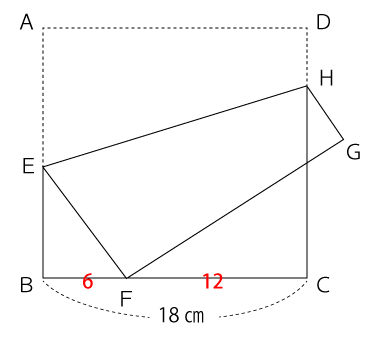
次に、BEの長さを求めていきます。
BE+EF=18なので、EFの長さは次のようにあらわすことができます。
EF=18-BE
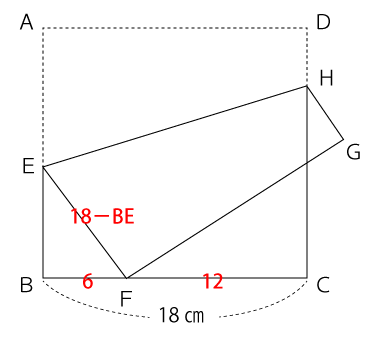
△EBFは直角三角形なので三平方の定理を利用してBEの長さを求めます。
EF²=BE²+BF²
(18-BE)²=BE²+6²
324-36BE+BE²=BE²+36
324-36BE=36
36BE=288
BE=8
よって、EF=18-8=10となります。
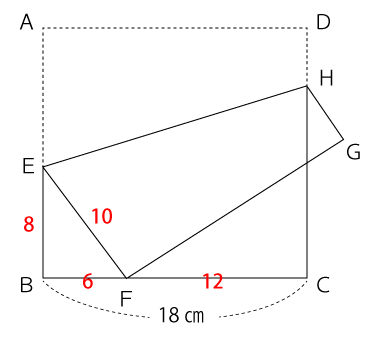
辺FGと辺CDの交点をPとした場合、△EFBと△FPCに着目します。
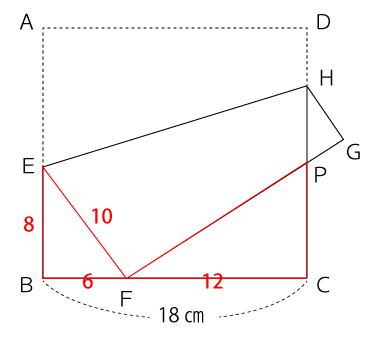
∠BEF=∠CFP、∠EFB=∠FPC、∠B=∠Cとなり、三角形の相似条件の1つである『2組の角が等しいとき』を満たしているので△EFBと△FPCは相似な三角形になります。その相似比は次の通り。
EB:FC=8:12
=2:3
よって、FPの長さは次の通り。
EF:FP=2:3
10:FP=2:3
2FP=30
FP=15
FGは正四角形の辺なので18㎝とわかっています。よって、PGの長さは次の通り。
PG=18-15=3㎝
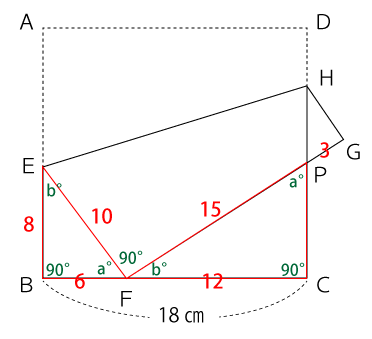
次に△FPCと△HPGに着目します。
∠FPCと∠HPGは対角なので同じ角度になります。また、∠C=∠G=90°なので三角形の相似条件の1つである『2組の角が等しいとき』を満たします。
よって、3つの三角形△EFBと△FPCと△HPGはいずれも相似な三角形になります。
△EFBと△HPGに着目し、相似比を求めます。BF=6、PG=3なので相似比は次の通り。
△EFB:△HPG=6:3
=2:1
よって、EBとHGの比も次のようになります。
EB:HG=2:1
よって、HGの長さは次の通り。
8:HG=2:1
2HG=8
HG=4
これで台形の面積を求めるための上底、下底、高さの3辺の長さが分かりました。
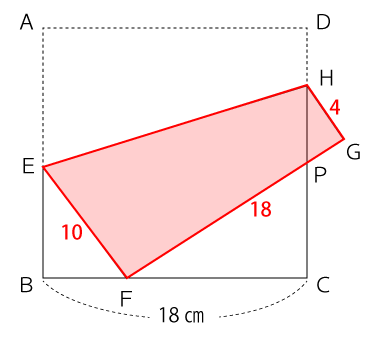
台形EFGHの面積は次の通り。
台形EFGHの面積=(上底+下底)×高さ÷2
=(4+10)×18÷2
=126
よって、求めたい四角形の面積は126㎝²
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。


∠BEF=∠CFP、∠EFB=∠FPCとなるのがよくわかりません。
教えていただけると幸いです。
まず、∠EFPは紙の角部分なので∠EFP=90°というのは分かります。
よって、
∠EFB=90°-∠CFP ・・・①
更に三角形内角の和は180°なので
∠BEF+∠EFB+∠B=180°となります。
∠Bは90°なので
∠BEF+∠EFB+90°=180°
∠BEF+∠EFB=90°
この式の∠EFBに①を代入します。
∠BEF+(90°-∠CFP)=90°
∠BEF-∠CFP=0
∠BEF=∠CFP
となります。
∠EFB=∠FPCも同じ考え方で導けます。
ただ、このように一つ一つ計算してると時間が全く足りなくなります。
この形は瞬時に△EFBと△FPCが相似な三角形になると判断できるようにしておく必要があります。