この問題は平成31年1月入校の東京都立職業能力開発センター入校選考試験問題の問2の(5)の解答と解説です。
問1および、問2の(1)~(4)に関しては以下のページに解説をまとめているので参考にして下さい。
実際の試験の問題用紙は以下のページで確認することができます。
試験問題 問2(5)
図の△ABCは、半径Rの円Oに接しています。AB=R、∠ABC=20°のとき、∠BACは何度であるか求めなさい。
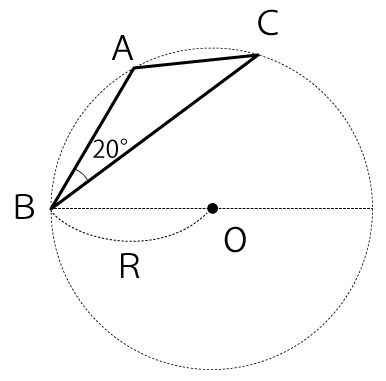
解答と解説
問2(5)の解答:130°
まずは、下図のように点Aと点Oを結ぶ線を引き△ABOを作ります。
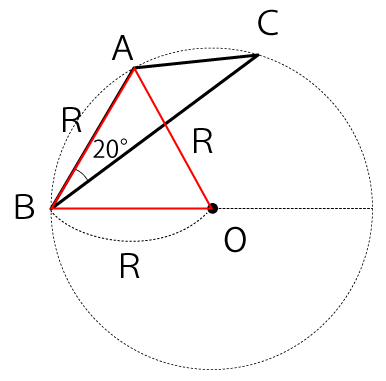
AOは半径なので△ABOは各辺の長さがRの正三角形だと分かります。よって、∠A、∠B、∠AOBはいずれも下図のように60°となります。
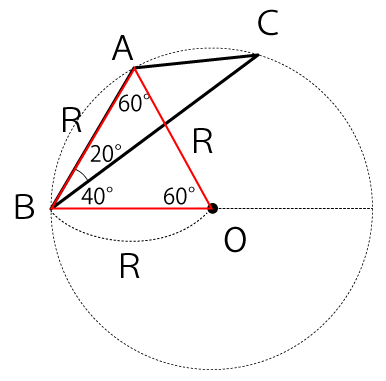
次に下図のように点Cと点Oを結んで△AOCを作ります。
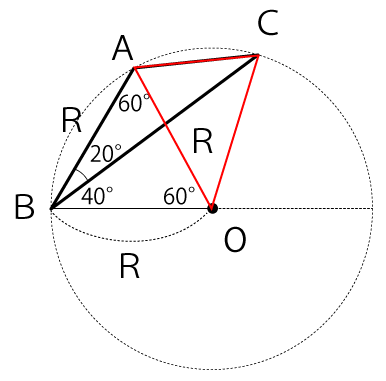
そうすると、△BOCは二等辺三角形なので∠OCB=40°だと分かります。よって、∠AOC=40°になります。
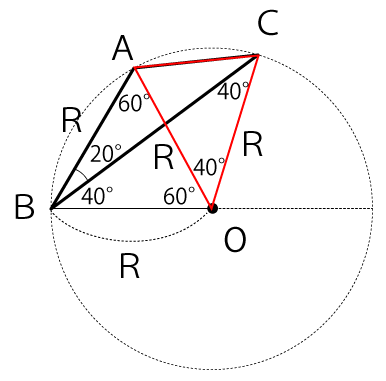
次に△AOCに着目します。△AOCは、AO=COで二等辺三角形になります。よって、∠OAC=70°だと分かります。
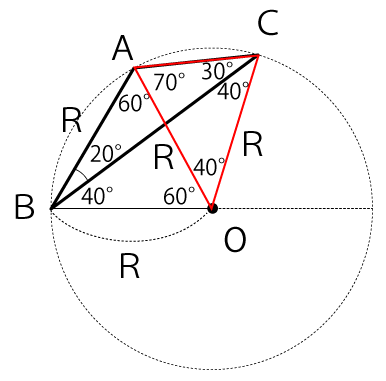
よって、求めたい∠BAC=60°+70°=130°
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。


4~5番目の図で∠AOC=40°がわかると、なぜ∠OAC=70°だと分かるのでしょうか?
この状態では∠ACBは不明なのではないですか?
ご質問ありがとうございます。
辺OAと辺OCはいずれも円の半径なので、長さが等しいことが分かります。よって、三角形AOCは二等辺三角形ということになります。
更に三角形AOCが二等辺三角形ということは、∠OAC=∠OCAが成り立ちます。
三角形の内角の和は180°なので、
∠AOC=40°
∠OAC=70°
∠OCA=70°
ということも分かります。