この問題は平成31年4月入校の東京都立職業能力開発センター入校選考試験問題の問1の解答と解説です。
問1および問2の(3)~(5)に関しては以下のページに解説をまとめているので参考にして下さい。
実際の試験の問題用紙は以下のページで確認することができます。
■目次
試験問題 問2(1)
歯の数が24枚である歯車Aと歯の数がX枚である歯車Bがあります。歯車Aと歯車Bをかみ合わせたとき、歯車Aを15回転させると、歯車Bは40回転しました。このとき、歯車Bの歯の数は何枚であるか求めなさい。
解答と解説
問2(1)の解答:9枚
歯車Aの歯数は24枚なので、15回転したとき歯車Bとの接点を360枚(24枚×15回転)の歯が通り過ぎたことになります。
同様に歯車Bの歯数はX枚なので、40回転したとき歯車Aとの接点を40X枚の歯が通り過ぎたことになります。
歯車Aと歯車Bの接点を通り過ぎた歯の枚数は同じはずなので以下の式が成り立ちます。
40X=360
この式を解けば求めたい歯車Bの歯数Xが求まります。
40X=360
X=9枚
試験問題 問2(2)
長さ324mの貨物列車が、ある鉄橋を渡り始めてから、渡り終えるまで64秒かかりました。また、長さ168mの急行列車が貨物列車の2倍の速さでこの鉄橋を渡り始めてから、渡り終わるまで24秒かかりました。このとき、鉄橋の長さは何mであるか求めなさい。
解答と解説
問2(2)の解答:300m
この問題を解くには距離と速度と時間の関係式を知っている必要があります。

求めたい鉄橋の長さをMと仮定します。
長さ324mの貨物列車が鉄橋を渡り切るには鉄橋の長さMに加え、貨物列車の長さ分だけ移動する必要があります。(橋の長さ分だけだと、貨物列車の先頭車両が鉄橋の出口に達しただけで、渡り切った状態ではない)
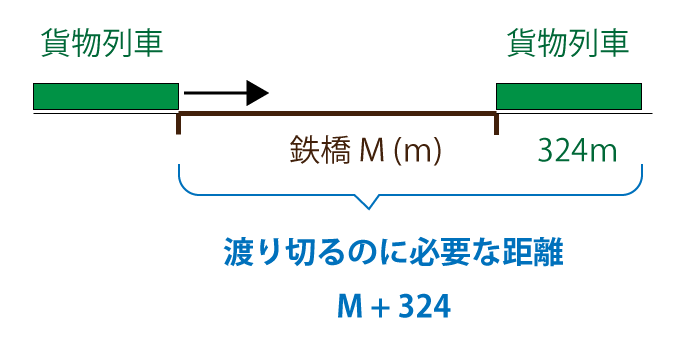
渡り終えるのにかかる時間:64秒
移動距離:M+324
よって、長さ324mの貨物列車の速度は次の通り。
速度=距離÷時間
=(M+324)÷64
次にこの速度の2倍の速さで長さ168mの急行列車が鉄橋を渡った場合、必要な移動距離はM+168で、渡り終えるのにかかる時間は24秒ということなので、次の式が成り立ちます。
距離=速度×時間
M+168=2×{(M+324)÷64}×24
M+168=48(M+324)/64
M+168=3(M+324)/4
4M+672=3M+972
4M-3M=972ー672
M=300
よって、鉄橋の長さは300m
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。


平成31年4月 2(2)の問題です。
回答例では、
① M+168=2×{(M+324)÷64}×24
から
② M+168=48(M+324)/64
となっていますが、計算の順序からみて、中カッコ内の計算が先だと
思うのですが、上記の①から②としたときに中カッコがなくなって
しまっています。
わたしとしては、
M+168=48{(M+324)÷64}
となり、(M+324)÷64の計算が先になると思って問題が解けません
でした。
なぜ、①から②へ進むときに中カッコがなくなっているのでしょうか。
よろしくお願いいたします。
川口様
回答遅くなり申し訳ございません。
川口様の考え方で正しいです。
①から②へいきなりとんでいますが、実際は川口様の考えられている通りの順の計算を行っています。
① M+168=2×{(M+324)÷64}×24
まず、最優先の計算は(M+324)ですよね。この時点ではMの値はまだわかりませんが、計算してM+324という数字だと考えます。そして、次に計算の優先順位としては『÷64』ですよね。M+324という数字を64で割ると次のような値になります。
(M+324)/64
かっこ内の計算はこれで終わりです。あとは、この(M+324)/64に残り2と24を掛けます。まずは、2をかけると次のようになります。
2×(M+324)/64
=2(M+324)/64
さらに上の値に24をかけます。
=24×2(M+324)/64
=48(M+324)/64
これを①式に当てはめると②の式になります。
② M+168=48(M+324)/64
どうでしょうか?分かりますでしょうか?