この問題は平成31年4月入校の東京都立職業能力開発センター入校選考試験問題の問2の(3)と(4)の解答と解説です。
問1および、問2の(1)(2)(5)(6)に関しては以下のページに解説をまとめているので参考にして下さい。
実際の試験の問題用紙は以下のページで確認することができます。
■目次
試験問題 問2(3)
図のような直角三角形があります。すべての辺に接するように円をかきます。このとき、円の面積は何cm²であるか求めなさい。
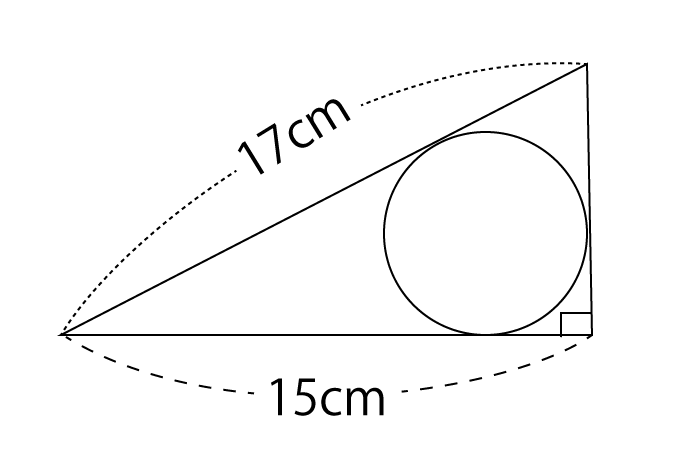
解答と解説
問2(3)の解答:9π cm²
この問題は、内接円の半径を求める公式を覚えていれば時間をかけずに解けるのですが、覚えている人は少ないと思います。よって、公式を利用せず解く方法で解説していきます。公式を利用したい人は『内接円の半径を求める式』などで検索するとすぐに見つかると思います。
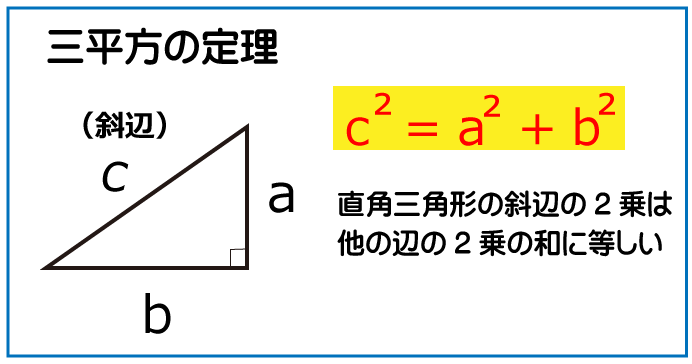
しかし、この問題を解くには三平方の定理は知っている必要があります。どの都道府県でも職業訓練の試験問題で三平方の定理を利用する問題が出題される可能性は非常に高いため必ず覚えておいてください。
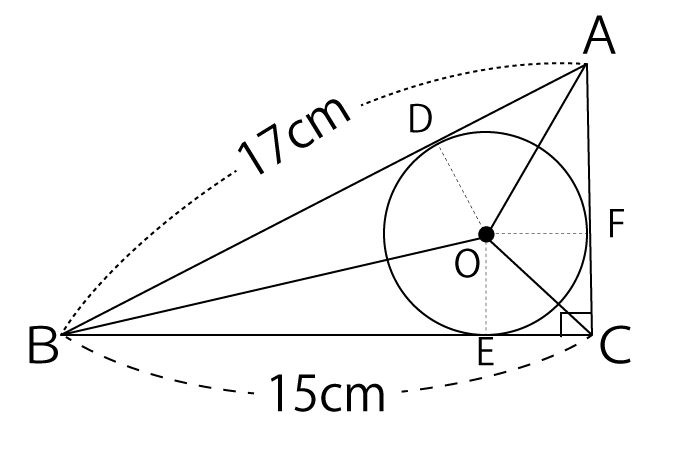
まず、下図のように三角形の各頂点をABCとし、円の中心をOとした場合、三角形ABCの中に△AOB、△BOC、△AOCの3つの三角形ができます。また、内接円の中心から各接線に引いた線は直角に交わるため、線分OD、OE、OFは△AOB、△BOC、△AOCの高さになります。
辺ACの長さは三平方の定理より、次の通り。
AB²=BC²+AC²
17²=15²+AC²
289=225+AC²
AC²=64
AC=8
よって、三角形ABCの面積は次の通り。
三角形ABCの面積=15×8÷2
=60 cm²
また三角形ABCの面積は次のようにあらわすこともできます。
△ABC=△AOB+△BOC+△AOC
△AOB、△BOC、△AOCの高さは円の半径なので、仮にRと仮定します。そうすると、半径Rは次のようになります。
△ABC=△AOB+△BOC+△AOC
60=(17×R÷2)+(15×R÷2)+(8×R÷2)
60=40R÷2
60=20R
R=3
円の半径が求まったので、円の面積も求められます。
円の面積=3×3×π=9π cm²
試験問題 問2(4)
100円硬貨が4枚、50円硬貨が5枚、10円硬貨が10枚あるとき、これらの硬貨を使って400円にする方法は、全部で何通りであるかを求めなさい。ただし、1枚も使わない硬貨があってもよいこととします。
解答と解説
問2(4)の解答:9通り
100円硬貨を基準に考えていきます。
(1)100円を4枚使うとき
100円×4枚
の1通り
(2)100円を3枚使うとき
(100円×3枚)+(50円×2枚)
(100円×3枚)+(50円×1枚)+(10円×5枚)
(100円×3枚)+(10円×10枚)
の3通り
(3)100円を2枚使うとき
(100円×2枚)+(50円×4枚)
(100円×2枚)+(50円×3枚)+(10円×5枚)
(100円×2枚)+(50円×2枚)+(10円×10枚)
の3通り
(4)100円を1枚使うとき
(100円×1枚)+(50円×5枚)+(10円×5枚)
(100円×1枚)+(50円×4枚)+(10円×10枚)
の2通り
(4)100円を0枚のとき
400円にはならない
よって、全部で1+3+3+2=9通り
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

