この問題は平成31年4月入校の東京都立職業能力開発センター入校選考試験問題の問2の(5)の解答と解説です。
問1および、問2の(1)~(4)に関しては以下のページに解説をまとめているので参考にして下さい。
実際の試験の問題用紙は以下のページで確認することができます。
試験問題 問2(5)
図は1辺の長さが4cmの立方体です。Aから辺BCを通り辺FGを通過してHまでひもをかけます。最も短いひもをかけたとき、このひもの長さは何cmになるか求めなさい。
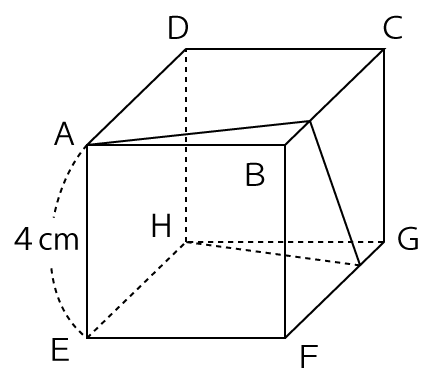
解答と解説
問2(5)の解答:4√10 cm
この問題は、図を展開することさえできれば難しい問題ではありません。
下図が実際に展開した図です。赤線がひもの部分で、最も短くなるのはAHが真っすぐ直線で結ばれる時です。
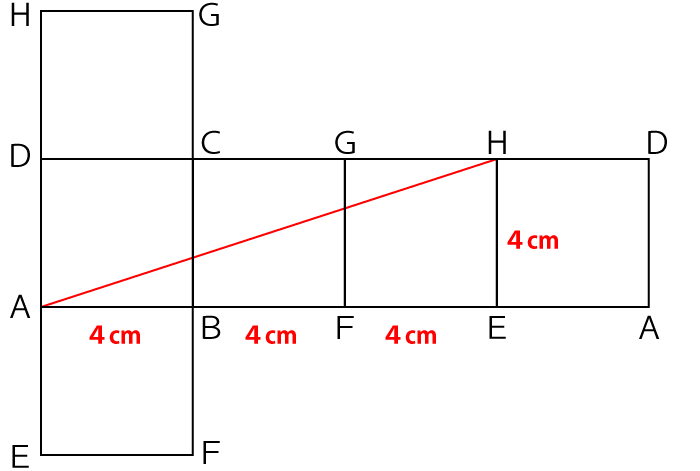
ここまでできれば、あとは三平方の定理を利用すれば簡単に解くことができますよね。
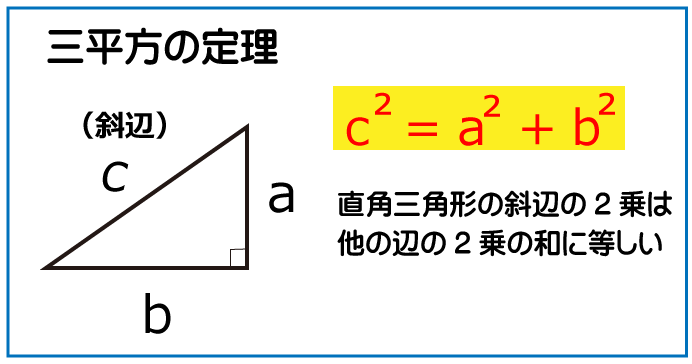
△AEHは12cmと4cmの辺を持つ直角二等辺三角形です。よって、AHの長さは次の通りになります。
AH²=AE²+HE²
AH²=12²+4²
AH²=144+16
AH²=160
AH=√160
AH=4√10
よって、最も短くなるひもの長さは、4√10 cm
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

