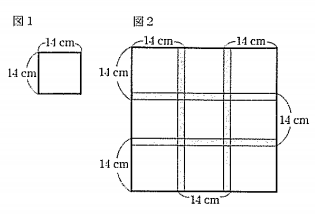
右の図1のような1辺が14cmの正方形の紙を貼り合わせて、大きな正方形をつくります。
図2は、図1の正方形の紙を9枚貼り合わせて大きな正方形の紙をつくったものです。貼り合わせた部分の幅は一定の長さとします。
このとき、次の各問の答えとして正しいものをア～オの中から１つ選び、記号で答えなさい。
[問題１]貼り合わせた部分の幅をＸcmとしたとき、図2の大きな正方形の1辺の長さを、Ｘを使って表しなさい。
ア 24-2Ｘ
イ 24+2Ｘ
ウ 42+2Ｘ
エ 42-2Ｘ
オ 84-4Ｘ
[問題２]図1の正方形の紙を何枚か貼りあわせて、大きな正方形の紙をつくったところ、正方形の周囲の長さが336cmになりました。貼りあわせた部分の幅が4cmであるとき、貼りあわせた正方形の紙の枚数をもとめなさい。
ア 36枚
イ 49枚
ウ 64枚
エ 81枚
オ 100枚
解答と解説
問題１の解説：
図2の正方形の1辺は、図1の1辺が14cmの小さな正方形3つで構成されています。よって、それら貼り付けたときの長さは、
14cm x 3つ ＝ 42cm
となります。しかし、貼りあわせた部分が2か所あり、その貼りあわせた部分の幅はＸcmなので、
Ｘcm x 2か所 ＝ 2Ｘ
だけ短くなります。よって、この貼りあわせた部分の幅2Ｘを42cmから引いてやれば図2の1辺の長さが出てきます。よって、求める解答は、42-2Ｘのエとなります。
解答：エ
問題２の解説：
正方形の周囲が336cmになるという事は、1辺の長さは
正方形の1辺の長さ＝336÷4＝84cm ・・・（１）
となることが分かります。また、問題1からも分かるように図1の正方形を3つ貼りあわせた場合は、2か所の貼りあわせ箇所ができます。4つ貼りあわせた場合は、3か所できます。よって、正方形の1辺に使われる図1の付け位の枚数をＮとした場合、貼りあわせ箇所は次の式で表すことができます。
貼りあわせ箇所の数 ＝ Ｎ － 1
更に貼りあわせた部分の幅が4cmということなので、貼りあわせた部分の合計幅は次の通りになります。
貼りあわせた部分の合計幅 ＝（Ｎ－1）x 4cm
＝ 4Ｎ－4 ・・・（２）
更に、1辺が14cmの正方形をＮ枚横に並べた時の長さは、
14cm x Ｎ ＝ 14Ｎ
となります。この14Ｎから貼りあわされた部分の合計幅（２）を引いてやると求めたい正方形の1辺の長さが算出できます。
14Ｎ－(4Ｎ－4)＝10Ｎ+4
この10Ｎ+4が最初にもとめた正方形の1辺の長さ84cmとなるはずなので、次のことが言えます。
10Ｎ＋4＝84
この式を解くと
10Ｎ+4＝84
10Ｎ＝80
Ｎ＝8
これで、求めたい正方形の1辺に使われる図1の小さな正方形の枚数が8枚と分かりました。正方形全体に使われる枚数は、横の枚数ｘ縦の枚数で算出できます。今回の問題は正方形なので横も縦も同じ枚数になります。よって、正方形全体の枚数は、
(横の枚数)ｘ(縦の枚数)
＝8枚ｘ8枚＝64枚
よって、求める解答は、64枚のウとなります。
解答：ウ
