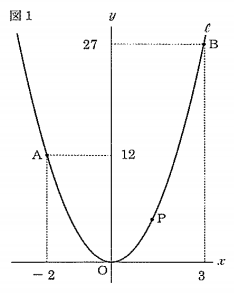
h26-9-2-q4-1右の図1で、曲線ℓは関数y=ax²（aは定数）のグラフです。2点Ａ(-2, 12)、Ｂ(3, 27)は曲線ℓ上にあります。曲線ℓ上を点Ａから点Ｂまで動く点をＰとします。

このとき、次の各問の答えとして正しいものをア～オの中から1つ選び、記号で答えなさい。

[問題１]点ＰのＸ座標が1の時、点Ａと点Ｐを通る直線の方程式を求めなさい。

[解答群]
ア　y=-2x+6
イ　y=3x+6
ウ　y=-3x+6
エ　y=-6x+6
オ　y=2x+6

[問題２]点Ｐが、ｙ軸について点Ａと対象の位置にあるとき、△ＯＡＰをｙ軸について回転しました。このときできる立体の体積を求めなさい。ただし、座標1目盛りを1cmとします。

[解答群]
ア　36Πcm³
イ　64Πcm³
ウ　24Πcm³
エ　16Πcm³
オ　18Πcm³

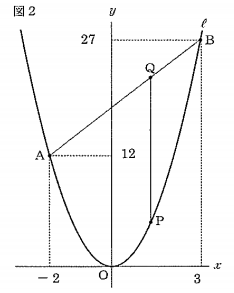試験問題 放物線[問題３]右の図2は、図1において、点Ｐを通り、ｙ軸に平行な直線が線分ＡＢと交わる点をＱとしたものです。

点ＰのＸ座標が正の数で、ＰＱ＝12となるとき、点Ｐの座標を求めなさい。

[解答群]
試験問題 解答


解答と解説

問題１の解説：
まずは、曲線ℓの式がy=ax²となっており、定数ａが分かっていないので先に求めます。この曲線ℓは、点Ａ(-2, 12)を通るので、曲線の式にこの座標を代入します。

　y=ax²
　12=a(-2)²
　12=4a

よって、ａ＝3とわかり、曲線ℓの式は

　y=3x² ・・・（１）

となります。点ＰのＸ座標は1ということなので、この曲線（１）にＸ座標1を代入すると、点Ｐのｙ座標が3だという事がわかります。よって、点Ｐの座標は(1, 3)。

この点Ａ(-2, 12)と点Ｐ(1, 3)を通る直線の式を求めます。直線の式は、y=ax+b で表されます。この直線の式にＡ点、Ｐ点の座標を代入することで、直線ＡＰの式が分かります。

点Ａ(-2, 12)を通る事より

　y=ax+b
　12=-2a+b ・・・（２）

点Ｐ(1, 3)を通る事より

　y=ax+b
　3=a+b
　b=3-a ・・・（３）

（３）を（２）に代入することでａが求まります。

　12=-2a+(3-a)
　12=-3a+3
　3a=-9
　a=-3

この時点で傾きaが―3となるのは解答ウしかないのでウと分かりますが、念のためbも求めます。式（２）か（３）どちらかにこのa=-3を代入するとbが出てきます。

　b=3-a
　b=3-(-3)
　b=6

よって、求める直線ＡＰは、y=-3x+6のウとなります。

解答：ウ

問題２の解説：
この問題を解くには、円錐の体積を求める公式を知っている必要があります。

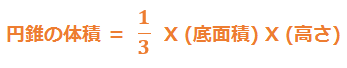
　円錐の体積

更に、円錐の底面は円なので円の面積を求める公式も知っておく必要があります。

　円の面積 ＝（半径）ｘ（半径）ｘ Π

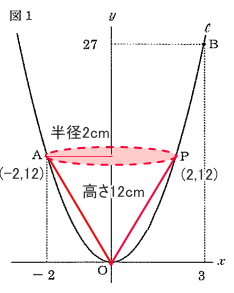h26-9-2-q4-5点Ｐをｙ軸を対象とした位置に点Ａがあるということなので、点Ｐの位置は図のような位置になります。更にこれでできた三角形ＯＡＰをｙ軸を中心として回転させた場合、直線ＡＰを直径とした円を底面として持つ円錐ができます。また、円の半径は、点Ａからｙ軸までの距離なので2とわかります。

底面となる円の面積は、上記の公式より

　円の面積(円錐の底面積) ＝（半径）ｘ（半径）ｘ Π
　　　　　　　　　　　　 ＝ 2 x 2 x Π
　　　　　　　　　　　　 ＝ 4Π

となります。次に円錐の体積を求めるのですが、高さは、12と分かっているので円錐の体積を求める公式より

　円錐の体積 ＝ 1/3 x 4Π x 12
　　　　　　 ＝ 16Π cm³

解答：エ

問題３の解説：
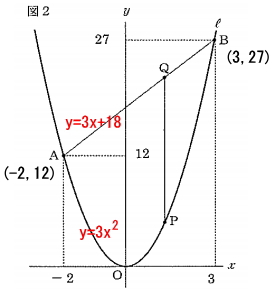
h26-9-2-q4-3
まずは、直線ＡＢの式はを求めます。求め方は問題１と同様です。2点Ａ(-2, 12)、Ｂ(3, 27)を通るので、直線の式y=ax+bより、

点Ａ(-2, 12)を通るとき

　12=-2a+b ・・・（４）

点Ｂ(3, 27)を通るとき

　27=3a+b
　b=27-3a ・・・（５）

式（４）に（５）を代入します。

　12=-2a+27-3a
　5a=15
　a=3

ａ＝３と分かったので、このａの値を式（５）に代入しｂを求めます。

　b=27-3×3=18

よって、直線ＡＢの式は、y=3x+18 だと分かります。更に点Ｐは、放物線y=3x²上にあるので、点ＰのＸ座標をＬとした場合、ｙ座標は3Ｌ²となります。

　点Ｐの座標 （Ｌ, 3Ｌ²）

また、点ＱのＸ座標は点ＰのＸ座標と同じなのでＬとなります。点Ｑは直線ＡＢ上にあるので、直線ＡＢの式y=3x+18にＬを代入すると、点Ｑのｙ座標は3Ｌ+18となります。

　点Ｑの座標 （Ｌ, 3Ｌ+18）　

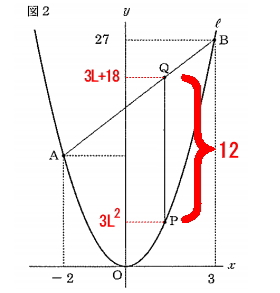h26-9-2-q4-4ここで2点ＰＱの座標がわかりました。次にこの2点のＰＱの長さを求めるのですが、設問よりＰＱ＝12となることが分かっています。

線分ＰＱは、ｙ軸と並行なので、Ｑのｙ座標とＰのｙ座標を引いた値が12になればいいわけです。よって、計算式は次の通り。
　(Ｑのｙ座標)－(Ｐのｙ座標)＝12
　(3Ｌ＋18)－(3Ｌ²)＝12
　3Ｌ＋18－3Ｌ²＝12
　－3Ｌ²＋3Ｌ＋18－12＝0
　－3L²＋3L＋6＝0
　L²－L－2＝0

この式を因数分解すると下記のようになります。

　(L-2)(L+1)＝0

因数分解のやり方はここでは割愛しますが、頻繁に出題されるのでできるようにはなっておきましょう。分からない方は、『因数分解』や『たすき掛け』といった単語で検索すると色々解説しているサイトが見つかると思います。

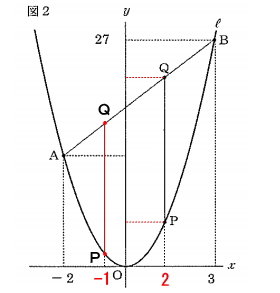h26-9-2-q4-5よって、ＰのＸ座標Ｌは2と-1の2つの解があることが分かります。何故、2つ解があるかと言うと図のように線分ＰＱの長さが12となるＰの座標が2つ存在するからです。

しかし、設問に「点ＰのＸ座標は正の数」とあるので、点ＰのＸ座標は2の方のみとなります。この時点で解答群には点ＰのＸ座標が2となるのはウしかないので解答はウだと分かります。

念のため、ｙ座標も確認します。点Ｐの座標 （Ｌ, 3Ｌ²）なので、ｙ座標は、

　3ｘ2²＝12

となります。よって、求める解答は点Ｐ(2, 12)のウ。

解答：ウ

※解説の内容が分からない場合はコメント下さい。