大阪 職業訓練 試験問題 数学-問3(平成27年2月19日実施)

平成27年2月19日に大阪で実施された職業訓練校の入校試験問題と解説です。大阪で行われる職業訓練は、面接と選考試験問題の両方で合否が判定されます。選考試験問題は選択問題ですがSPIよりも少し難易度が高めに設定されています。これらの過去問を繰り返し実施し、解けるようにしておきましょう。

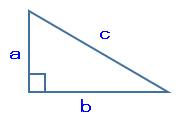
次の図のように、長方形ABCDを頂点Cを中心にして、時計回りにゆっくりと回転させる。AB＝4cm、BC＝8cmとする。このとき、次の各問の答えとして正しいものをア～オの中から1つ選び、記号で答えなさい。但し、円周率はπとする。

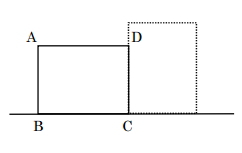
[問題１]頂点 A がえがく曲線の長さを求めなさい。

[問題２]辺ACが通る部分の面積はいくらですか。

解答と解説

問題１の解説：

長方形ABCDを頂点cを中心に時計回りに回転させると次の図のように円を描いて回転します。

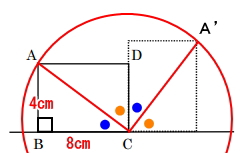
このときできる円の半径はACと同じ。よって、点AからA’までの円の円周を求めることで移動した距離がわかります。

∠ACA’は、●＋● で四角形の1角と同じなので90°です。よって、求めたい点AからA’までの円周は、円の1/4(90÷360)の扇形の円周ということになります。

円の円周を求めるためには、まずは円の半径であるACの長さを求める必要があります。そこで、利用するのが三角定理です。三角形ABCは直角三角形なので、三角定理を使用すると次のようになります。

　ｃ²＝ａ²＋ｂ²
　AC²＝4²＋8²
　AC²＝16＋64
　AC²＝80
　AC＝√80
　AC＝√4²×5
　AC＝4√5

半径が出てきました。次に円の円周を求めます。円周を求める公式は次の通り。

　円周＝直径×Π

半径は、4√5なので、直径は8√5となります。よって、公式より円周は次の通り。

　円周＝8√5Π

更に扇形ACA’は、円の1/4の大きさの扇型なので、AA’の距離は上の円周の1/4の長さとなります。

　AA’の長さ＝8√5Π × 1/4
　　　　　＝2√5Π

解答：ア

問題２の解説：
辺ACが通る部分の面積というのは、扇形ACA’の面積になります。よって、問題１と同じようにまずは、円の面積を求め、最後にその面積を1/4すれば扇形の面積が出てきます。

　円の面積＝半径×半径×Π

半径は、ACの長さ4√5なので、円の面積は次の通り。

　円の面積＝半径×半径×Π
　　　　　＝(4√5)×(4√5)×Π
　　　　　＝80Π

円の面積が出てきました。よって、扇形の面積は次の通り。

　扇形の面積＝80Π × 1/4
　　　　　　＝20Π cm²

解答：エ

※解説内容に不明な点があればコメント欄にコメントください。