大阪 職業訓練 試験問題 数学-問4(平成27年2月19日実施)

大阪の職業訓練の選考試験問題と解説です。本問題は平成27年2月19日に実施された試験問題です。大阪で行われる職業訓練の試験問題は、筆記試験ではなく選択方式。問題4は図形の問題でSPIよりも難易度が少々高めです。過去問を繰り返し実施し、解けるようにしておきましょう。

次の図のように1辺の長さが8㎝の立方体ABCD‐EFGHがある。頂点Fから対角線AGに垂線をひき、AGとの交点をPとするとき、以下の問いに答えなさい。

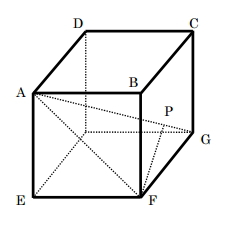
[問題１] 対角線AGの長さを求めなさい。

[問題２] △AFGの面積を求めなさい。

[問題３] 線分FPの長さを求めなさい。

解答と解説

問題１の解説：
この問題を解くには、三平方の定理と三角比を利用します。

三平方の定理
下図ような直角三角形がある場合、3つの辺の長さの関係は次の式で表すことができます。

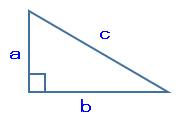
　ｃ²＝ａ²＋ｂ²

三角比
下図のような直角二等辺三角形がある場合、各辺の長さの比は次の比で表すことができます。

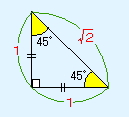
三平方の定理を使えば、この三角比は覚えていなくても求めることができますが、覚えておいた方が問題を解く時間短縮につながります。

それでは問題を解いていきます。

求め方の流れとしては、三角形AEGの∠E＝90°なので、辺EGの長さがわかれば三平方の定理を利用して辺AGの長さを求めることができます。よって、まずは辺EGの長さを求めます。

辺EGは三角形EFGの斜辺です。また、三角形EFGは直角二等辺三角形なので三角比が利用できます。

　EF：FG：EG＝1：1：√2

が成り立つのでEF＝FG＝8cmということは、

　EF：FG：EG＝8：8：8√2

となり、EGの長さは8√2と分かります。

辺EGの長さがわかったので、三平方の定理を利用して辺AGの長さを求めます。

　ｃ²＝ａ²＋ｂ²
　AG²＝AE²＋EG²
　AG²＝8²＋(8√2)²
　AG²＝64＋128
　AG²＝192
　AG＝√192
　AG＝√4²×12
　AG＝4√12
　AG＝4√2²×3
　AG＝8√3

解答：エ

問題２の解説：
∠AFG＝90°なので、三角形AFGの底辺は辺FGで8cm、高さはAFとなります。AFは問題1で求めたEGと同じ長さなので8√2です。

よって、三角形AFGの面積は

　三角形ＡＦＧの面積＝8×8√2÷2
　　　　　　　　　　＝32√2

解答：エ

問題３の解説：
この問題は相似比を使ってもとめることができます。2つの三角形が相似になる条件は頭にいれておきましょう。

2つの三角形が相似になる条件

• 3組の辺の比が等しい
• 2組の辺の比が等しく、そのはさむ角が等しい
• 2組の角が、それぞれ等しい

三角形AFGと三角形FPGを見てください。

　三角形AFGの∠AFGは、90°
　三角形FPGの∠FPGは、90°

更に三角形AFGの∠FGA と三角形FPGの∠FPGの∠PGFは同じ場所なので同角となります。よって、三角形の相似条件『2組の角が、それぞれ等しい』が当てはまるので、この2つの三角形は相似と言えます。
　

では、この三角形AFGと三角形FPGの相似比は？

三角形AFGのAGに相当するのが、三角形FPGのFGです。AGは問題1で求めており、8√3です。FGは、8cmと分かっているので、2つの三角形の相似比は次の通り。

　三角形AFG：三角形FPG＝8√3：8

これは、三角形FPGは、三角形AFGの1/√3ということになります。

そして、求めたいのは三角形FPGのPFの長さ。ここに相当するのが三角形AFGのAFに該当します。AFの長さも8√2と分かっているので、PFの長さは、このAFの長さの1/√3ということになります。

よって、PFの長さは

　ＰＦの長さ＝AF × 1/√3
　　　　　　＝8√2 × 1/√3
　　　　　　＝8√2/√3

ＰＦの長さがでました。しかし、解答群に求めた解答がありません。これは、分母の√3をなくすために少し変形をさせています。通常、分母にルートを残すのはよくないとされているのでこのような変形が必要となっています。

ではどのように変形させるのか？

√3/√3 を掛けてやります。これは約分すると1なので、実質は1を掛けているのと同じであり、あくまで変形されるだけでこれにより答えの大きさが変わるようなことはありません。

　ＰＦの長さ＝8√2/√3
　　　　　　＝8√2/√3 × √3/√3
　　　　　　＝8√6/3
　　　　　　

解答：オ

※解説の内容が分からない場合はコメント下さい。