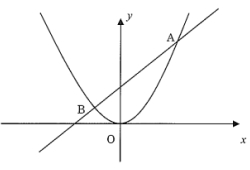
 図のグラフは、放物線y=ax² と直線y=x+3 が点A、Bで交わっている。点Aのx座標が3である。このとき次の問に答えなさい。
図のグラフは、放物線y=ax² と直線y=x+3 が点A、Bで交わっている。点Aのx座標が3である。このとき次の問に答えなさい。
[問題1]点Aのy座標を求めなさい。
ア 6
イ 7
ウ 8
エ 9
オ 10
[問題2]aの値を求めなさい。
ア 1/3
イ 2/3
ウ 4/3
エ 5/3
オ 1
[問題3]点O、A、Bを直線で結ぶと三角形ができる。この三角形の面積を求めなさい。
ア 27/4
イ 29/4
ウ 45/4
エ 3
オ 6
解答と解説
問題1の解説:
点Aのx座標が3と分かっているので、直線の式y=x+3 のxに3を代入すればy座標を求めることができます。
y=x+3 にx=3 を代入すると
y=3+3=6
よって、求めるy座標は6のア
解答:ア
問題2の解説:
A点の座標が(3、6)と分かったので、放物線の式にxとyを代入すればaの値が求まる。
y=ax² にy=6、X=3 を代入すると
6=a×(3)²
6=9a
a=6/9=2/3
よって、求めるaの値は、2/3のイ
解答:イ
問題3の解説:
A点の座標(3、6)、O点の座標(0、0)と分かっているので残るB点の座標を求める必要があります。求め方は、放物線のグラフの式と直線の式が分かっているので連立方程式で解きます。
放物線の式: y=(2/3)X²
直線の式: y=X+3
直線の式を放物線の式に代入します。
X+3=(2/3)X²
分数のままだと計算が面倒になるので両辺に3を掛けて分数をなくします。
3X+9=2X²
この式のXを求めると、B点のX座標がでてきます。
3X+9=2X²
2X²-3X-9=0
(2X+3)(X-3)=0
X=3、-3/2
X=3は、A点のX座標なのでB点のX座標は-3/2
よって、y座標は直線の式y=X+3 にこのX座標を代入すれば求めることができます。
y=-3/2 + 3=-3/2 + 6/2=3/2
よって、B点の座標は(-3/2、3/2)
さて、ここから三角形OABの面積を求めるのだが、求め方は公式を利用する方法と、利用しない方法の2通りあります。まずは、公式を利用する方法。
公式を利用して解く方法
3つの座標の内、1点が原点(0,0)を通り、残り2点を(a,b)、(c,d)とした場合、次の公式で面積が求められます。
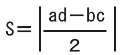
O点(0、0)
A点(3、6)
B点(-3/2、3/2)
公式に値を代入し求めていきます。
S={3×3/2 - 6x(-3/2)} / 2
=(9/2 + 9) / 2
=(27/2) / 2
=27/4
よって、求める面積は、27/4のア
公式を利用しない解き方
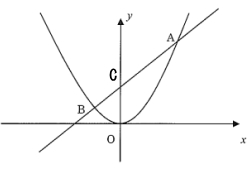 図の様に直線とy軸の交点をCとします。
図の様に直線とy軸の交点をCとします。
そして、面積は三角形OCBと、三角形OCAの2つに分けて考えます。
まず、三角形OCBですが底辺をOCとした場合高さはB点からy軸に向かって垂直に下ろした線が高さになります。要は、B点のX座標が三角形の高さです。B点のX座標は-3/2です。高さとしてはマイナスを除いた3/2です。
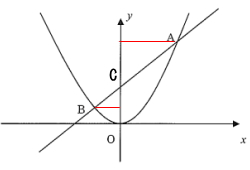
底辺の長さはC点のy座標、直線の式y=x+3 にX=0を代入してyを求めてもいいですが、直線の式の切片がy座標なのでX=0を代入しなくても即座に3とわかります。
よって、三角形OCBの面積は
三角形OCBの面積=底辺×高さ÷2
=3×(3/2)÷2
=9/4
次に三角形OCAの面積を求めるのですが、底辺は同様にOCで長さは3となります。高さはA点からy軸に向かって垂直に下ろした線の長さです。要は、A点のX座標です。A点のX座標は3と分かっているので三角形OCAの高さは3になります。(参照:補足事項1)
よって、三角形OCAの面積は
三角形OCAの面積=底辺×高さ÷2
=3×3÷2
=9/2
これで、三角形OCBとOCAの面積が求まりました。この2つを足すと、三角形OABの面積となります。
三角形OABの面積=三角形OCBの面積+三角形OCAの面積
=9/4 + 9/2
=9/4 + 18/4
=27/4
よって、三角形OABの面積は27/4のア
解答:ア
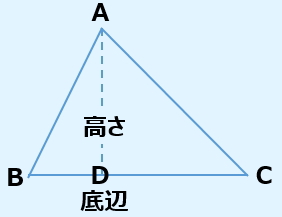
三角形の面積は、下記の式で表すことができます。有名な公式ですよね?
三角形ABCの面積=BC×AD÷2
では、下図の様な三角形の面積はどうなるのか? 三角形の面積を求める公式は利用できるのか?
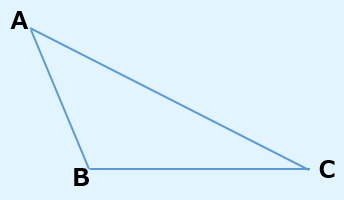
多くの人は、三角形の面積を求めるにあたり、次のように考えるのではないでしょうか?
三角形ABCの面積=AC×BD÷2
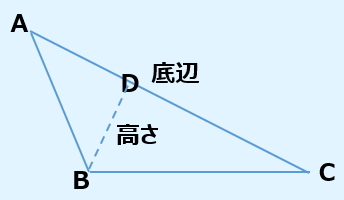
しかし、下図のように考えることもできます。
三角形ABCの面積=BC×AD÷2
これが、『えっ!? そうなの?』と思われた方は、三角形の面積の公式の本来の意味を理解していない方だと思われます。そもそも、三角形の面積の公式はなぜ、
底辺×高さ÷2
なのか?これは、四角形(平行四辺形)の面積を求める公式『底辺×高さ』が応用されています。下図の様に全く同じ三角形ABCを2つ用意します。
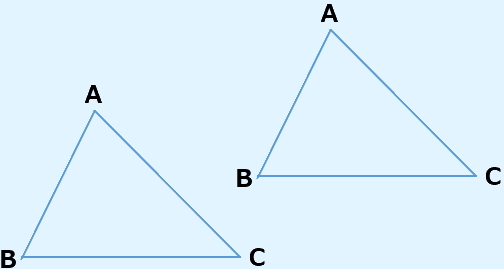
次に一方の三角形を180度回転させます。
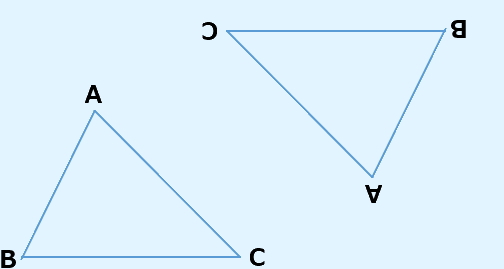
そして、お互いの三角形を下図の様にくっつけると、平行四辺形が出来上がります。

平行四辺形の面積は、『底辺BC×高さAE』ですよね。この平行四辺形は、全く同じ三角形ABCを二つくっつけて作ったものなので、三角形ABCの面積は、平行四辺形の面積の半分『底辺BC×高さAE÷2』となります。これが三角形の面積の公式の意味になります。
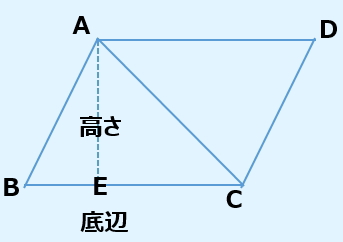
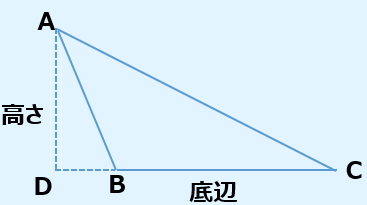
上が理解できていれば、下図も理解できると思います。
三角形ABCの面積=BC×AD÷2

同様のことをすると、下図のように平行四辺形ができあがります。平行四辺形の面積は『底辺BC×高さAD』。よって、三角形ABCの面積は、次のように表すことができます。
三角形ABCの面積=BC×AD÷2
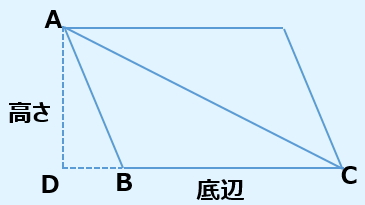
※解説の内容が分からない場合はコメント下さい。


三角形OCAの面積を求める所が分かりません。公式を使わないパターンの方です。
三角形の面積を求める方程式の
底辺×高さ÷2
を当てはめているようですが、それでいいんですか?
OCAの三角形の形が、上記の方程式では求めれらないんじゃないんですか?
また、
問題3の解説
で、「この式のXを求めると、B点のX座標がでてきます。」
とありますが、
何故B点のX座標が出てくるんですか?
直線の式が関わってるからなんですか?
コメントありがとうございます。
>OCAの三角形の形が、上記の方程式では求めれらないんじゃないんですか?
⇒三角形の面積を求める公式は、どんな形であれ三角形であればあてはめることはできます。ページの下部の方に[補足事項1]を追記したのでご確認お願いします。
>何故B点のX座標が出てくるんですか?
⇒これは、連立方程式の意味を理解する必要があるのですが、今回の様に
放物線の式: y=(2/3)X²
直線の式: y=X+3
の2つのグラフの式の連立方程式を解くということは、二つのグラフの交点座標AとBを求めることを意味します。