(4)下図の四角形ABCDにおいて、BC=11cm、CD=5cm、AD=7cm、∠A=90°、∠B=90°である。このとき、四角形ABCDの面積を求めなさい。

解答と解説
試験問題の解答:27 cm²
分かっていることを図に記載すると下図のようになります。
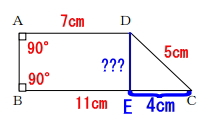
この四角形ABCDは台形なので、面積を求めるには台形の面積の公式を使用します。
(下底の長さ+上底の長さ) × 高さ ÷ 2
ここで、下底の長さは辺BCで11cm、上底の長さは辺ADで7cmと分かります。しかし、高さが現時点では不明。そこで高さを求める必要があるのですが、点Dから辺BCへ垂直に下ろした線を辺DEとします。この辺DEの長さが高さとなります。
そして、辺DEの長さを求めるには、三角形DECに着目します。三角形DECは直角三角形で2辺の長さが分かっているので三平方の定理を使用することができます。
※三平方の定理
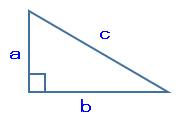
a²+b²=c²
DC²=DE²+EC²
5²=DE²+4²
25=DE²+16
DE²=9
DE=3
これで、台形の高さも出てきました。よって、台形の面積は次の通り。
(下底の長さ+上底の長さ) × 高さ ÷ 2
(11+7)×3÷2=27

