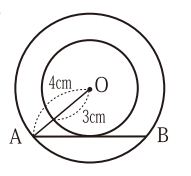
(5)下の図のように、同じ点Oを中心とする半径3cmと4cmの2つの円がある。小さい円に接する大きい円の弦ABの長さを求めなさい。
解答と解説
試験問題の解答:2√7 cm
この問題を解くには、三平方の定理を使う必要があります。
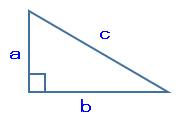
三平方の定理とは、上図の様な直角三角形がある場合、次の式が成り立ちます。
c²=a²+b²
これを抑えた上で、問題を解いていきます。下図の様に中心Oから円の弦に向かって垂直に下ろし、弦と交わる点をCとします。
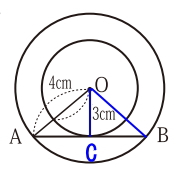
この時、OCは、小さい円の半径なので長さは、3cmとわかります。さらに三角形AOCと三角形BOCは、辺OCが共通で長さが等しく、辺OAと辺OBも大きい円の半径となるので長さが等しい、また、∠OCAと∠OCBは90°で2つの三角形は、直角三角形だとわかります。よって、直角三角形AOCと三角形BOCは合同(等しい三角形)と言えます。
よって、『辺ACの長さ=辺BCの長さ』も成り立ちます。
※直角三角形の合同条件
2つの直角三角形の斜辺とその他の1辺の長さが等しければ、その2つの直角三角形は合同と言える。
2つの直角三角形の斜辺とその他の1辺の長さが等しければ、その2つの直角三角形は合同と言える。
次に直角三角形OACの2辺の長さが分かっているので、ここで三平方の定理を使用し残り1辺の長さも求めます。残り1辺ACの長さをbとした場合、次のようになります。
c²=a²+b²
4²=3²+b²
b²=16-9=7
b=√7
弦ABの長さは、ACの2倍の長さなので
弦ABの長さ=2×√7=2√7cm

