平成27年5月21日に大阪で実施された職業訓練の選考試験問題 問3の解説です。大阪で行われる職業訓練の試験問題は、筆記試験ではなく毎回、選択方式ですが試験時間が短いためこれらの過去問を繰り返し実施し、短時間かつ正確に解けるようにしておきましょう。
問1~2、問4に関しては以下のページに解説をまとめているので参考にして下さい。
大阪 職業訓練 試験問題 数学-問1
大阪 職業訓練 試験問題 数学-問2
大阪 職業訓練 試験問題 数学-問4
次の図において、直線ℓは Y=(4/5)X+(6/5)で、原点を頂点とする2次関数と2点B、Dで交わっている。直線ℓとx 軸との交点をA、y軸との交点をCとするとき、線分の長さについて、AB:BC=1:2 が成り立つ。このとき、次の各問の答えとして正しいものをア~オの中から1つ選び、記号で答えなさい。
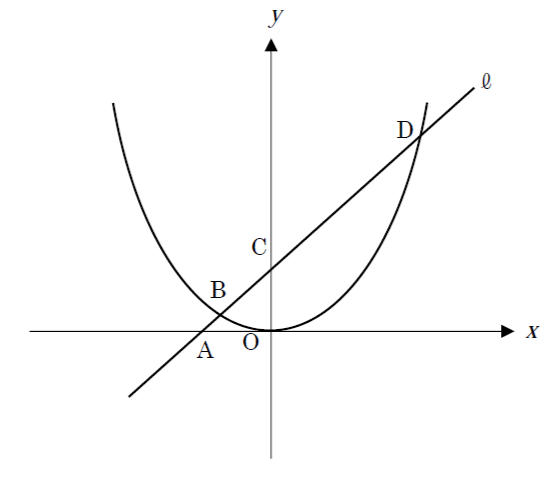
[問題1] 2次関数の式を求めなさい。
[解答群]
ア Y=X² イ Y=(1/5)X² ウ Y=(2/5)X² エ Y=(3/5)X² オ Y=(4/5)X²
[問題2] 三角形OBDの面積を求めなさい。
[解答群]
ア 2 イ 12/5 ウ 14/5 エ 16/5 オ 3
解答と解説
試験問題1の解答:ウ
まずは、点A、点Bの座標を考えていきます。
点Aの座標
点Aは、直線ℓ Y=(4/5)X+(6/5)とX軸との交点なので、Y座標は0になります。よって、直線ℓの式にY=0を代入すれば点AのX座標が求まります。
Y=(4/5)X+(6/5)
0=(4/5)X+(6/5)
-(4/5)X=(6/5)
-X=(6/5)x(5/4)
-X=3/2
X=-3/2
よって、点Aの座標は(-3/2,0) ・・・(1)
点Bの座標
下図のように点BからX軸に垂線を引き、X軸と交わる点をB’とします。
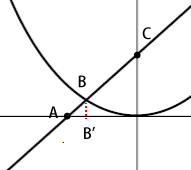
三角形ABB’と三角形ACOは3つの内角がそれぞれ等しいので相似な三角形です。相似な三角形は各辺の長さの比率も同じになります。設問よりAB:BC=1:2とわかっているので、同様にAB’:B’C=1:2も成り立ちます。
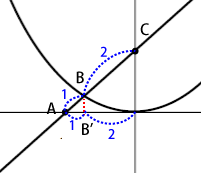
AB’:B’C=1:2ということは、点B’は線分AOを2/3した位置にあることがわかります。点AのX座標は-3/2なので、点B’の座標は次の通りになります。
(-3/2)x(2/3)=-1
よって、点B’の座標は(-1,0)
これは点BのX座標も-1ということを意味します。よって、点Bの座標は次の通り。
直線ℓ Y=(4/5)X+(6/5)
Y=(4/5)x(-1)+(6/5)
=-(4/5)+(6/5)
=2/5
よって、点Bの座標は(-1,2/5) ・・・(2)
2次関数について考える
2次関数の放物線の式は、原点Oが頂点となっているので傾きをaとした場合、次の式で表すことができます。
Y=aX²
また、この放物線は点B(-1,2/5)を通ることから傾きaは次のようになります。
Y=aX²
点B(-1,2/5)を通るので、X=-1、Y=2/5を代入する。
2/5=ax(-1)²
a=2/5
よって、2次関数の放物線のグラフの式は次の通り。
Y=(2/5)X²
試験問題2の解答:イ
点Dの座標を求める
点Dは、直線ℓ Y=(4/5)X+(6/5)と放物線Y=(2/5)X²の交点です。よって、次のように求めることができます。
Y=(4/5)X+(6/5) ・・・(1)
Y=(2/5)X² ・・・(2)
式(2)を式(1)へ代入する
(2/5)X²=(4/5)X+(6/5)
この式を解くと直線ℓと放物線のX座標の交点が求まります。
(2/5)X²=(4/5)X+(6/5)
(2/5)X²-(4/5)X-(6/5)=0
2X²-4X-6=0
X²-2X-3=0
(X-3)(X+1)=0
X=3,-1
点AのX座標が-1なので、点DのX座標は3だとわかります。直線ℓの式にこのX=3を代入すれば、点DのY座標の方も求まります。
Y=(4/5)X+(6/5)
=(4/5)x3+(6/5)
=18/5
よって、点Dの座標は(3,18/5)・・・(3)
三角形OBDの面積を求める
求め方としては、三角形OADの面積を求め、そこから三角形OABの面積を引く流れで行う。

[三角形OADの面積]
三角形OADの高さは点DからX軸に垂線を下した長さ。言い換えると、点DのY座標の値になります。よって、高さは18/5。底辺は線分AOなので、点AのX座標の値が底辺の長さになります。ただ、長さにマイナスはないのでマイナスを取り除いた3/2が底辺の長さとなります。よって、三角形OADの面積は次の通り。
面積=(3/2)x(18/5)÷2
=27/10
[三角形OABの面積]
三角形OABの高さは点BからX軸に垂線を下した長さ。言い換えると、点BのY座標の値になります。よって、高さは2/5。底辺は線分AOなので、点AのX座標の値が底辺の長さになります。ただ、長さにマイナスはないのでマイナスを取り除いた3/2が底辺の長さとなります。よって、三角形OABの面積は次の通り。
面積=(3/2)x(2/5)÷2
=3/10
[三角形OBDの面積]
△OBD面積=△OAD面積-△OAB面積
=(27/10)-(3/10)
=24/10
=12/5
※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容も不明であれば遠慮なくコメントください。

