この問題は平成30年度生の埼玉県立技術専門校短期コース入校試験問題の問8(問1~5は国語)の解答と解説です。
問7~問9に関しては以下のページに解説をまとめているので参考にして下さい。
実際の試験の問題用紙は以下のページで確認することができます。
必要な知識
- 三平方の定理
- 三角形の面積を求める公式
問8 試験問題
次の(1)、(2)の問いに答えなさい。
(1)下図の正八面体の展開図として正しいものは、次のうちどれか。1から5のうち番号で答えなさい。
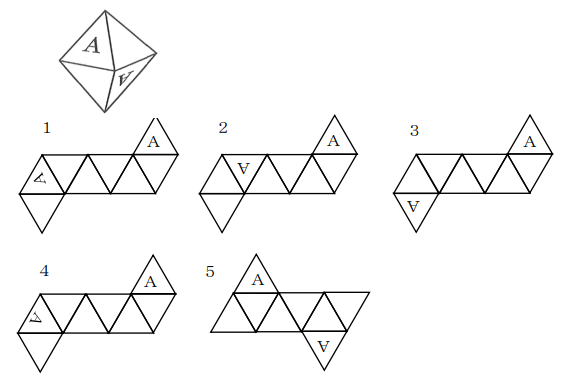
(2)下図の二等辺三角形ABCの面積を求めなさい。
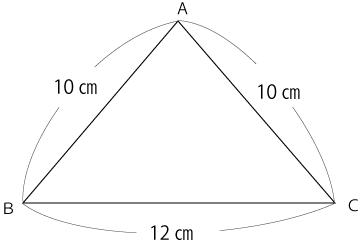
解答と解説
解答と解説を記載していきます。
解き方が分からないという人を少しでも減らすためにできる限り分かり易く必要以上に細かく順を追って解説している部分がありますが、実際の試験時は丁寧に計算し過ぎると時間のロスに繋がるため、自分の分かるところは効率よく解答していくようにしてください。
問題1の解答と解説
試験問題1の解答:1
この問題は計算など一切必要なく図を展開できれば解ける問題なのですが、こういった複雑な図形を頭の中で展開できる人は意外に少ないです。また、今回の問題の正八面体の場合、展開パターンが全部で11種類もあるためあらかじめ覚えておくというのも無理があります。
そこで今回のような問題の解き方を紹介しておきたいと思います。
まず、下図のように図形の背面をイメージできるように点線で記します。
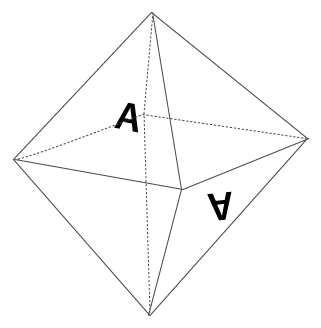
次に各頂点に番号やアルファベットの記入していきます。
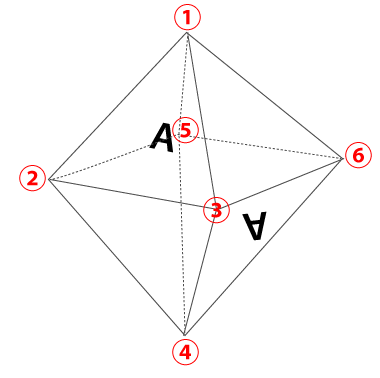
ここで割り当てた各頂点の番号に対比するように解答群の図形にも番号を振っていきます。上の図を参照しながら①から順に解答群の展開図に記載していくと書きやすいと思います。まずは、解答群の展開図1に書き込んでみます。
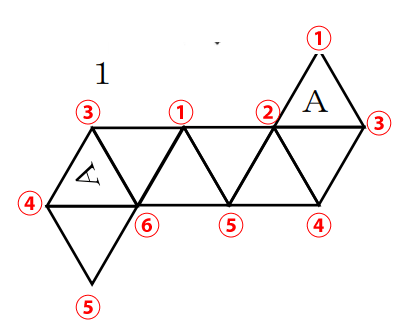
展開前の図形と比較して、Aが記されている面の頂点が共に①と④で一致しています。
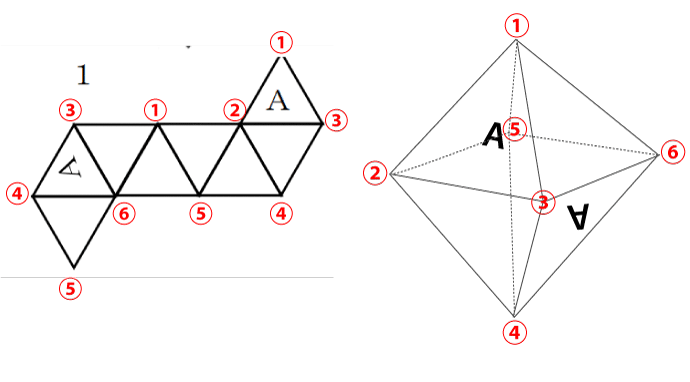
よって、答えは解答群の1となります。
問題2の解答と解説
試験問題2の解答:48㎝²
この問題を解くには三平方の定理を知っておく必要があります。三平方の定理とは以下の内容です。
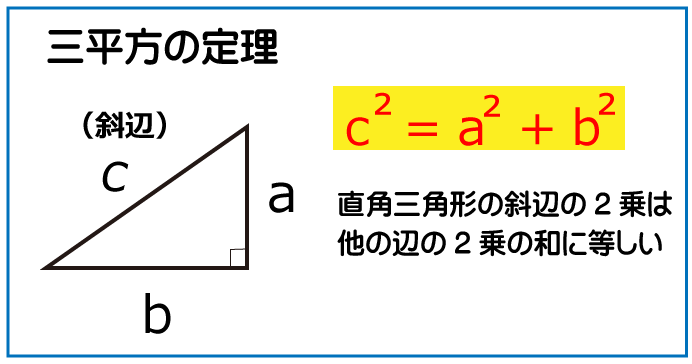
三角形の面積を求めるには高さが必要ですが、現時点では高さが分かっていません。
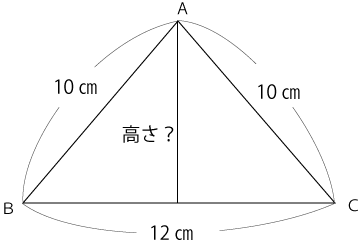
高さは二等辺三角形の頂点Aから辺BCに垂線を下ろした線なので下図のようになります。
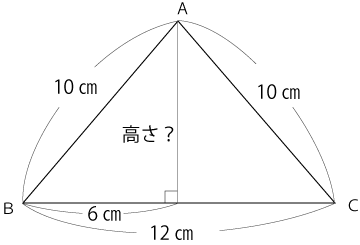
これで三平方の定理を使用すれば高さが求まります。
三平方の定理
10²=高さ²+6²
高さ²=100-36
高さ²=64
高さ=8㎝
よって、二等辺三角形の面積は次の通り。
二等辺三角形の面積=12×8÷2
=48㎝²
※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

