この問題は平成30年度生の埼玉県立技術専門校短期コース入校試験問題の問9(問1~5は国語)の解答と解説です。
問7~問9に関しては以下のページに解説をまとめているので参考にして下さい。
実際の試験の問題用紙は以下のページで確認することができます。
必要な知識
- 円周を求める公式
- 平行線と角度の関係
問9 試験問題
次の(1)、(2)の問いに答えなさい。
(1)下図は底面の半径が6㎝、母線の長さが10㎝の円すいである。この円すいの展開図で、側面となる扇形の中心角を求めなさい。
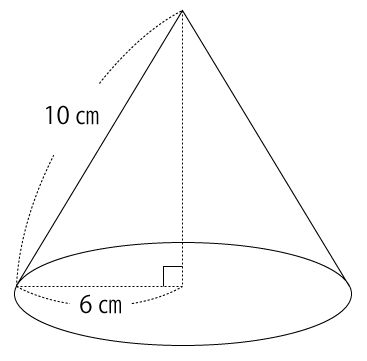
(2)下図の直線mと直線nは平行である。∠Xの角度を求めなさい。
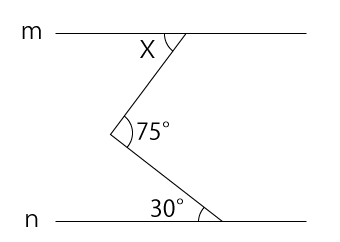
解答と解説
解答と解説を記載していきます。
解き方が分からないという人を少しでも減らすためにできる限り分かり易く必要以上に細かく順を追って解説している部分がありますが、実際の試験時は丁寧に計算し過ぎると時間のロスに繋がるため、自分の分かるところは効率よく解答していくようにしてください。
問題1の解答と解説
試験問題1の解答:216°
円すいを展開すると下図のようになります。そして、求めるのが扇形の中心角Xです。
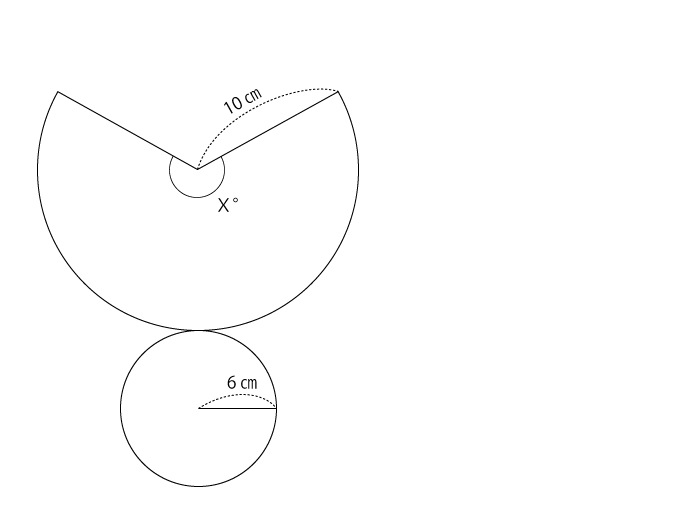
下図の赤線部分が円すいのときに接している部分です。
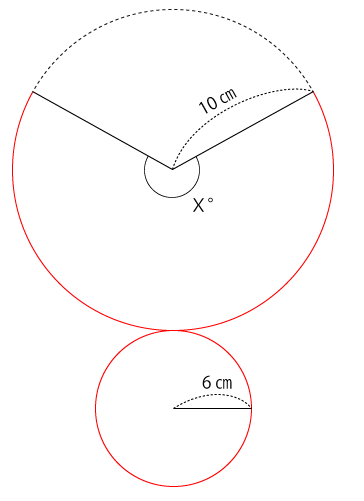
よって、円すいの底面である円の円周と扇形の円弧がの長さは等しいことになります。
底面の円の円周=(6+6)×π
=12π・・・①
扇形の円弧の長さも12πで同じですが、扇形が完全な円の場合の円周を求めます。
扇形の円の円周=(10+10)×π
=20π・・・②
扇形の円弧の大きさが完全な円に対してどれくらいの大きさかは①÷②で求まります。
扇形の円弧の大きさ=12π÷20π
=3/5
これにより扇形の円弧の大きさは半径10㎝の完全な円を3/5にした大きさということがわかります。よって、求めたい中心角は次の通り。
中心角X=360×3/5
=216°
問題2の解答と解説
試験問題2の解答:45°
平行線の錯角は等しいという点を知っていれば簡単に解ける問題です。錯角とは、下図のように直線mと直線nが平行なとき∠aと∠bの位置関係の角を言います。
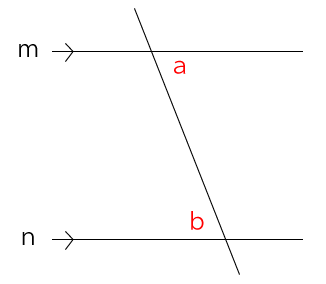
今回の問題も下図のように直線mとnに平行な線lを引き、下から順に錯角の角度を求めていくことで∠Xの角度がでてきます。
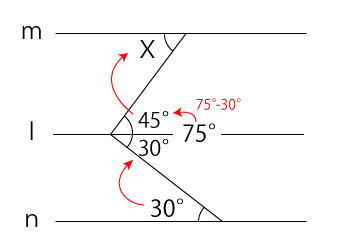
よって、∠X=45°
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

