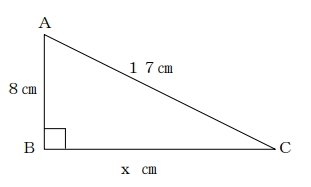
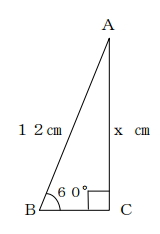
下の図で、xの値を求めなさい。
解答と解説
試験問題1の解答:x=15
この問題を解くには、三平方の定理を知っている必要があります。三平方の定理とは、
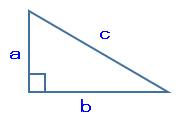
直角三角形の各辺の関係として、次の式が成り立ちます。
a²+b²=c²
これが分かっていれば、この問題は簡単ですね。
a=8cm
b=xcm
c=17cm
よって、求めたいxの長さは次の式で表すことができます。
8²+x²=17²
64+x²=289
x²=289-64
x²=225
x=±15
しかし、辺の長さにマイナスはありえないので、求めたいxの長さは次の通り。
x=15
試験問題2の解答:X=6√3
この問題を解くには三角比を知っている必要があります。
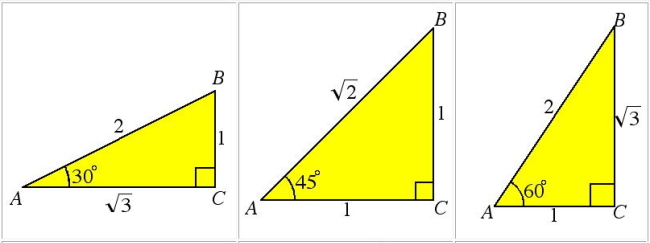
三角形の一角が30度、45度、60度のいずれかである直角三角形の各辺の比率は、上図のようになります。今回の問題であれば、一番右端図が該当し、各辺の比率は1:2:√3となります。
辺AB=12cm
辺AC=Xcm
これが上図の辺ABとBCにあてはまるので、辺の比率は2:√3と分かります。よって、次の比が成り立ちます。
12:X=2:√3
これを解くと次のようになります。
12:X=2:√3
2X=12√3
X=6√3
※解説の内容が不明、不十分というのがあればコメントをください。